Bài 73 trang 62 SGK giải tích 12 nâng cao, Cho hàm số Tìm điều kiện đối với p và q để hàm số f có một cực đại và một cực tiểu. b)...

Bài 73. Cho hàm số \(f\left( x \right) = {x^3} + px + q\)

a) Tìm điều kiện đối với p và q để hàm số f có một cực đại và một cực tiểu.

b) Chứng minh rằng nếu giá trị cực đại và giá trị cực tiểu trái dấu thì phương trình: \({x^3} + px + q = 0\,\,\left( 1 \right)\) có ba nghiệm phân biệt.

c) Chứng minh rằng điều kiện cần và đủ để phương trình (1) có ba nghiệm phân biệt là: \(4{p^3} + 27{q^2} < 0\)

a) Ta có \(f’\left( x \right) = 3{x^2} + p\)

\(f’\left( x \right) = 0 \Leftrightarrow 3{x^2} + p = 0\,\,\left( 1 \right)\)

Hàm số f có một cực đại và một cực tiểu khi và chỉ khi khi phương trình (1) có hai nghiệm phân biệt \( \Leftrightarrow p < 0\)

Khi đó hai nghiệm của (1) là: \(x =  – \sqrt { – {p \over 3}} ;\,\,\,x = \sqrt { – {p \over 3}} \)

Bảng biến thiên: 

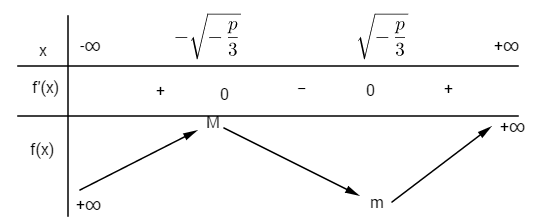
Với \(M = {\left( { – \sqrt { – {p \over 3}} } \right)^3} – p\sqrt { – {p \over 3}}  +q= q – {2 \over 3}p\sqrt { – {p \over 3}} \)

\(m = {\left( {\sqrt { – {p \over 3}} } \right)^3} + p\sqrt { – {p \over 3}}  + q = q + {2 \over 3}p\sqrt { – {p \over 3}} \)

b) Nếu Mm<0 và m < 0, khi đó, phương trình f(x) = 0 có ba nghiệm \(\alpha ,\,\beta ,\,\gamma \) với \(\alpha  <  – \sqrt { – {p \over 3}} ; – \,\sqrt { – {p \over 3}}  < \beta  < \sqrt { – {p \over 3}} \,\,\text{và}\,\,\gamma  > \sqrt { – {p \over 3}} \)

c) Nếu Mm > 0 thì hai số M và m cùng dấu.

Nếu M < 0 và m < 0 thì phương trình (1) có nghiệm duy nhất (Lớn hơn \(\sqrt { – {p \over 3}} \))

Nếu M > 0 và m > 0 thì phương trình (1) có nghiệm duy nhất ( Nhỏ hơn \(\sqrt { – {p \over 3}} \))

Vậy điều kiện cần và đủ để phương trình (1) có ba nghiệm phân biệt là: 

\(\left\{ \matrix{
p < 0 \hfill \cr
Mm = {q^2} – {4 \over 9}{p^2}\left( { – {p \over 3}} \right) < 0 \hfill \cr} \right. \Leftrightarrow 4{p^3} + 27{q^2} < 0\)