b) Tìm giao điểm của hai đường cong (P) và (H). Chứng minh rằng hia đường cong đó có tiếp tuyến chung tại giao điểm của chúng.
c) Xác định các khoảng trên đó (P) nằm phía trên hoặc phía dưới (H).. Bài 78 trang 62 SGK giải tích 12 nâng cao - Câu hỏi và bài tập chương I - Ứng dụng đạo hàm để khảo sát và vẽ đồ thị của hàm số
Bài 38.
a) Vẽ đồ thị (P) của hàm số \(y = {x^2} - x + 1\) và đồ thị (H) của hàm số \(y = {1 \over {x + 1}}\).
b) Tìm giao điểm của hai đường cong (P) và (H). Chứng minh rằng hia đường cong đó có tiếp tuyến chung tại giao điểm của chúng.
c) Xác định các khoảng trên đó (P) nằm phía trên hoặc phía dưới (H).

a) Đồ thị
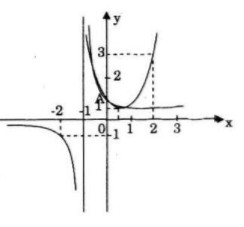
b) Hoành độ giao điể của parabol (P) và hypebol (H) là nghiệm của phương trình:
\({x^2} - x + 1 = {1 \over {x + 1}} \Leftrightarrow \left( {x + 1} \right)\left( {{x^2} - x + 1} \right) = 1\) (vì x = -1 không là nghiệm của phương trình)
\( \Leftrightarrow {x^3} + 1 = 1 \Leftrightarrow x = 0;\,\left( {y\left( 0 \right) = 1} \right)\)
Advertisements (Quảng cáo)
Giao điểm của (P) và (H) là A(0;1)
Đặt \(f\left( x \right) = {x^2} - x + 1;\,g\left( x \right) = {1 \over {x + 1}}\)
Ta có: \(f’\left( x \right) = 2x - 1;\,g’\left( x \right) = - {1 \over {{{\left( {x + 1} \right)}^2}}}\)
\(f’\left( 0 \right) = g’\left( x \right) = - 1\)
Suy ra (P) và (H) có tiếp tuyến chung tại A nên (P) và (H) tiếp xúc nhau tại điểm A.
c) Xét hiệu \(f\left( x \right) - g\left( x \right) = {x^2} - x +1 - {1 \over {x + 1}} = {{{x^3}} \over {x + 1}}\)
Bảng xét dấu f(x) – g(x)
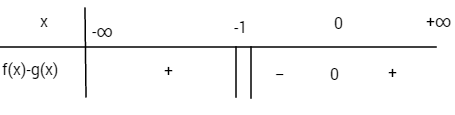
Trên các khoảng \(\left( { - \infty ; - 1} \right)\) và \(\left( {0; + \infty } \right)\) (P) nằm phía trên (H). Trên khoảng \(\left( { - 1;0} \right)\) (P) nằm phía dưới (H).
