a) Khảo sát sự biến thiên và vẽ đồ thị của hàm số với m = 2.
b) Tìm các giá trị của m sao cho đồ thị của hàm số cắt trục hoành tại bốn điểm, tạo thành ba đoạn thẳng có độ dài bằng nhau.. Bài 75 trang 62 SGK giải tích 12 nâng cao - Câu hỏi và bài tập chương I - Ứng dụng đạo hàm để khảo sát và vẽ đồ thị của hàm số
Bài 75. Cho hàm số: \(y = {x^4} - \left( {m + 1} \right){x^2} + m\)
a) Khảo sát sự biến thiên và vẽ đồ thị của hàm số với m = 2.
b) Tìm các giá trị của m sao cho đồ thị của hàm số cắt trục hoành tại bốn điểm, tạo thành ba đoạn thẳng có độ dài bằng nhau.

a) Với \(m=2\) hàm số đã cho có dạng: \(y={x^4} - 3{x^2} + 3\)
Tập xác định: \(D=\mathbb R\)
\(\eqalign{
& y’ = 4{x^3} - 6x \cr
& y’ = 0 \Leftrightarrow \left[ \matrix{
x = 0 \hfill \cr
x = {{\sqrt 6 } \over 2} \hfill \cr
x = - {{\sqrt 6 } \over 2} \hfill \cr} \right. \cr} \)
Hàm số đồng biến trên khoảng: \(\left( { - {{\sqrt 6 } \over 2};0} \right)\) và \(\left( {{{\sqrt 6 } \over 2}; + \infty } \right)\)
Hàm số nghịch biến trên khoảng: \(\left( { - \infty ; - {{\sqrt 6 } \over 2}} \right)\) và \(\left( {0;{{\sqrt 6 } \over 2}} \right)\)
Cực trị:
Hàm số đạt cực đại tại \(x=0;\,\,y(0)=2\)
Hàm số đạt cực tiểu tại \(x = {{\sqrt 6 } \over 2}\) và \(x = - {{\sqrt 6 } \over 2}\), \(y\left( { \pm {{\sqrt 6 } \over 2}} \right) = - {1 \over 4}\)
Giới hạn: \(\mathop {\lim }\limits_{x \to \pm \infty } y = + \infty \)
Bảng biến thiên:
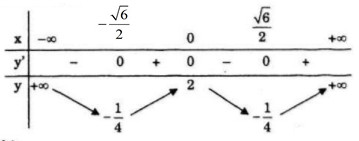
Advertisements (Quảng cáo)
Đồ thị:
Đồ thi cắt tung độ tại điểm \((0;2)\)
Đồ thị cắt hoành độ tại 4 điểm: \(\left( { - \sqrt 2 ;0} \right),\left( { - 1;0} \right)\left( {1;0} \right),\left( {\sqrt 2 ;0} \right)\)
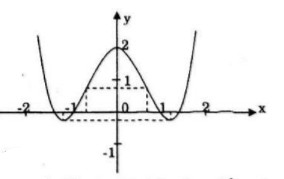
Đồ thị hàm số là hàm chẵn nhận trục Oy làm trục đối xứng.
b) Hoành độ giao điểm của đường cong (C) và trục là nghiệm phương trình
\({x^4} - \left( {m + 1} \right){x^2} + m = 0\,\,\,\left( 1 \right)\,\,\, \Leftrightarrow \left[ \matrix{
{x^2} = 1 \hfill \cr
{x^2} = m \hfill \cr} \right.\)
(1) có 4 nghiệm phân biệt khi và chỉ khi m>0 và \(m \ne 1\)
Khi đó (1) có 4 nghiệm: \(x = - 1;\,x = 1;\,x = - \sqrt m ;\,x = \sqrt m \)
* \( - \sqrt m < - 1 < 1 < \sqrt m \)
(C) cắt trục tại 4 điểm tạo thành ba đoạn thẳng bằng nhau khi \(\sqrt m - 1 = 1 - \left( { - 1} \right) = 2 \Leftrightarrow m = 9\)
* \( - 1 < - \sqrt m < \sqrt m < 1\)
(C) cắt trục hoành tại 4 điểm tạo thành ba đoạn thẳng bằng nhau khi \(1 - \sqrt m = \sqrt m - \left( { - \sqrt m } \right) = 2\sqrt m \)
Vậy m= 9 hoặc \(m = {1 \over 9}\)
