Bài 1. Cho hàm số:
\(f(x) = ax^2– 2(a + 1)x + a + 2 ( a ≠ 0)\)
a) Chứng tỏ rằng phương trình f(x) = 0 luôn có nghiệm thực. Tính các nghiệm đó.
b) Tính tổng \(S\) và tích \(P\) của các nghiệm của phương trình \(f(x) = 0\). Khảo sát sự biến thiên và vẽ đồ thị hàm số của \(S\) và \(P\) theo \(a\).
Ta có:
\(f(x) = ax^2– 2(a + 1)x + a + 2 = (x – 1)(ax – a- 2)\) nên phương trình \(f(x) = 0\) luôn có hai nghiệm thực là:
\(x = 1, x = {{a + 2} \over a}\)
Theo định lí Vi-et, tổng và tích của các nghiệm đó là:
\(S = {{2a + 2} \over a},P = {{a + 2} \over a}\)
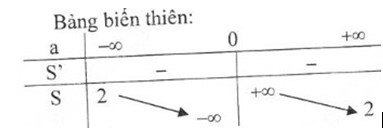
1. Khảo sát sự biến thiên và vẽ đồ thị hàm số \(S = {{2a + 2} \over a} = 2 + {2 \over a}\)
- Tập xác định : \((-∞, 0)∪ (0, +∞)\)
- Sự biến thiên: \(S’ = - {2 \over {{a^2}}} < 0,\forall a \in ( - \infty ,0) \cup (0, + \infty )\) nên hàm số nghịch biến trên hai khoảng \((-∞, 0)\) và \((0, +∞)\)
- Cực trị: Hàm số không có cực trị
- Giới hạn tại vô cực và tiệm cận ngang
\(\eqalign{
& \mathop {\lim }\limits_{a \to + \infty } S = \mathop {\lim }\limits_{a \to + \infty } (2 + {2 \over a}) = 2 \cr
& \mathop {\lim }\limits_{a \to - \infty } S = \mathop {\lim }\limits_{a \to - \infty } (2 + {2 \over a}) = 2 \cr} \)
Vậy \(S = 2\) là tiệm cận ngang
- Giới hạn vô cực và tiệm cận đứng:
Advertisements (Quảng cáo)
\(\eqalign{
& \mathop {\lim }\limits_{a \to {0^ + }} S = \mathop {\lim }\limits_{a \to {0^ + }} (2 + {2 \over a}) = + \infty \cr
& \mathop {\lim }\limits_{a \to {0^ - }} S = \mathop {\lim }\limits_{a \to {0^ - }} (2 + {2 \over a}) = - \infty \cr} \)
Vậy \(a = 0\) là tiệm cận đứng.
- Bảng biến thiên:
Đồ thị hàm số:
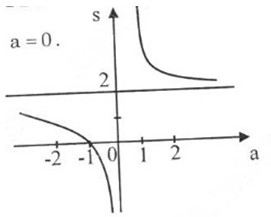
Đồ thị không cắt trục tung, cắt trục hoành tại \(a = -1\)
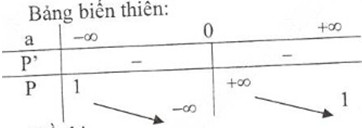
2) Khảo sát sự biến thiên và vẽ đồ thị hàm số \(P = {{a + 2} \over a} = 1 + {2 \over a}\)
Tập xác định: \(D = \mathbb R\backslash {\rm{\{ }}0\} \)
\(S’ = {{ - 2} \over {{a^2}}} < 0,\forall a \in D\)
\(\mathop {\lim }\limits_{a \to {0^ - }} S = - \infty ⇒ \)Tiệm cận đứng: \(a = 0\)
\(\mathop {\lim }\limits_{a \to \pm \infty } S = 1⇒\) Tiệm cận ngang: \(S = 1\)
Đồ thị hàm số:
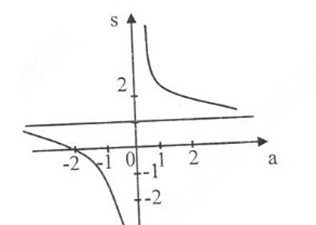
Ngoài ra: đồ thị hàm số \(P = {{a + 2} \over a} = 1 + {2 \over a}\) có thể nhận được bằng cách tịnh tiến đồ thị \(S = {{2a + 2} \over a} = 2 + {2 \over a}\) dọc theo trục tung xuống phía dưới \(1\) đơn vị.
