Advertisements (Quảng cáo)
Cho hàm số : y = x3 + ax2 + bx + 1
a) Tìm a và b để đồ thị của hàm số đi qua hai điểm A(1, 2) và B(-2, -1)
b) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số ứng với các giá trị tìm được của a và b.
c) Tính thể tích vật thể tròn xoay thu được khi quay hình phẳng giới hạn bởi các đường thẳng y = 0, x = 0, x = 1 và đồ thị (C) quanh trục hoành.
a) Đồ thị hàm số đi qua hai điểm A(1, 2) và B (-2, -1) khi và chỉ khi:
\(\left\{ \matrix{
2 = 1 + a + b + 1 \hfill \cr
– 1 = – 8 + 4a – 2b + 1 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
a = 1 \hfill \cr
b = – 1 \hfill \cr} \right.\)
b) Khi a = 1, b = -1 ta có hàm số: y = x3 + x2 – x + 1
_ Tập xác định: (-∞, + ∞)
_ Sự biến thiên: y’ = 3x2 + 2x – 1
y’= 0 ⇔ x = -1, x = \({1 \over 3}\)
Trên các khoảng (-∞, -1) và \(({1 \over 3}, + \infty )\) , y’>0 nên hàm số đồng biến
Trên khoảng \(( – 1,{1 \over 3})\) , y’ < 0 nên hàm số nghịch biến
_ Cực trị: Hàm số đạt cực đại tại x = -1, yCD = 2
Hàm số đạt cực tiểu tại \(x = {1 \over 3},{y_{CT}} = {{22} \over {27}}\)
_ Giới hạn tại vô cực: \(\mathop {\lim }\limits_{x \to + \infty } y = + \infty ;\mathop {\lim }\limits_{x \to – \infty } y = – \infty \)
Bảng biến thiên:
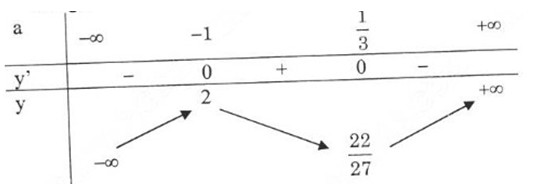
Đồ thị hàm số:
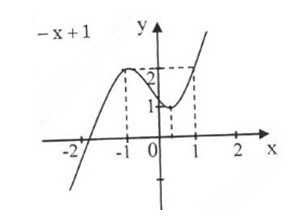
Đồ thị cắt trục tung tại y = 1, cắt trục hoành tại x ≈ -1, 84
c) Trong khoảng (0, 1) ta có y > 0.
Vì vậy, thể tích cần tìm là:
\(V = \pi \int_0^1 {({x^3}} + {x^2} – x + 1{)^2}dx = {{134\pi } \over {105}}\)