Bài 10. Cho hình chóp \(S.ABC\) có bốn đỉnh đếu nằm trên một mặt cầu, \(SA = a, SB = b, SC = c\) và ba cạnh \(SA, SB, SC\) đôi một vuông góc. Tính diện tích mặt cầu và thể tích khối cầu được tạo bởi mặt cầu đó

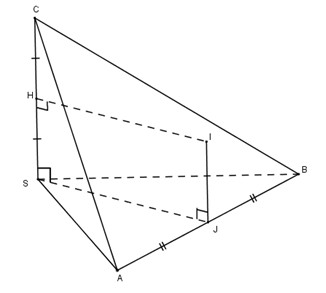
Gọi \(I\) là tâm cầu ngoại tiếp hình chóp tam giác \(S.ABC\). Hạ \(IJ\) vuông góc \((SAB)\), vì \(J\) cách đều \(3\) điểm \(S, A, B\) nên \(J\) cũng cách đều \(3\) điểm \(S, A, B\).
Vì tam giác \(SAB\) vuông đỉnh \(S\) nên \(J\) là trung điểm của \(AB\).
Ta có \(SJ ={1 \over 2}AB = {1 \over 2}\sqrt {{a^2} + {b^2}}\)
Do \(SC\) vuông góc \((SAB)\) nên \(IJ // SC\).
Gọi \(H\) là trung điểm \(SC\), ta có \(SH = IJ = {c \over 2}\).
Advertisements (Quảng cáo)
Do vậy, \(I{S^2} = I{J^2} + S{J^2} = {{({a^2} + {b^2} + {c^2})} \over 4}\) và bán kính hình cầu ngoại tiếp \(S.ABC\) là
\(r = IS = {1 \over 2}\sqrt {{a^2} + {b^2} + {c^2}} \)
Diện tích mặt cầu là:
\(S = 4\pi {r^2} = \pi ({a^2} + {b^2} + {c^2})\)
Thể tích khối cầu là :
\(V = {4 \over 3}\pi {r^3} = {1 \over 6}\pi {\left( {{a^2} + {b^2} + {c^2}} \right)^{{3 \over 2}}}\).
