Cho hàm số \(y = {{x - 2} \over {x + m - 1}}\)
a) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số khi m = 2
b) Viết phương trình tiếp tuyến d của đồ thị (C) tại điểm có hoành độ a ≠ -1.
a) Khi m = 2, ta có hàm số: \(y = {{x - 2} \over {x + 1}}\)
_ Tập xác định: (-∞, -1) ∪ (-1, +∞)
_ Sự biến thiên: \(y’ = {3 \over {{{(x + 1)}^2}}} > 0,\forall x \in ( - \infty , - 1) \cup (1, + \infty )\)
nên hàm số đồng biến trên hai khoảng này.
_ Hàm số không có cực trị
_ Giới hạn tại vô cực và tiệm cận ngang
Advertisements (Quảng cáo)
\(\mathop {\lim }\limits_{x \to + \infty } y = \mathop {\lim }\limits_{x \to + \infty } {{x - 2} \over {x + 1}} = 1;\mathop {\lim }\limits_{x \to - \infty } y = \mathop {\lim }\limits_{x \to - \infty } {{x - 2} \over {x + 1}} = 1\)
Nên x = -1 là tiệm cận đứng.
Bảng biến thiên:
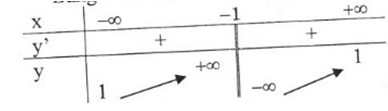
Đồ thị hàm số:
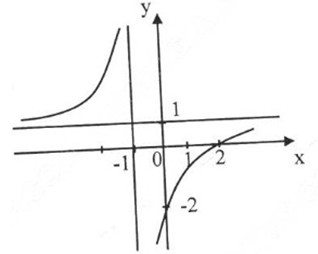
Đồ thị cắt trục tung tại y = -2, cắt trục hoành tại x = 2
b) Tiếp tuyến của đồ thị (C) tại điểm M có hoành độ a≠-1 có phương trình:
\(y = y'(a)(x - a) + y(a) = {3 \over {{{(a + 1)}^2}}}(x - a) + {{a - 2} \over {a + 1}}\)
