Bài 7. Một hình trụ có bán kính \(r\) và chiều cao \(h = r\sqrt3\).
a) Tính diện tích xung quanh và diện tích toàn phần của hình trụ.
b) Tính thể tích khối trụ tạo nên bởi hình trụ đã cho.
c) Cho hai điểm \(A\) và \(B\) lần lượt nằm trên hai đường tròn đáy sao cho góc giữa đường thẳng \(AB\) và trục của hình trụ bằng \(30^0\). Tính khoảng cách giữa đường thẳng \(AB\) và trục của hình trụ

Theo công thức ta có:
\(S_{xq} = 2πrh = 2\sqrt3 πr^2\)
\(S_{tp} = 2πrh + 2πr^2 = 2\sqrt3 πr^2 + 2 πr^2 \)
\(= 2(\sqrt3 + 1)πr^2\) ( đơn vị thể tích)
Advertisements (Quảng cáo)
b) \(V\)trụ = \(πR^2h = \sqrt3 π r^3\)
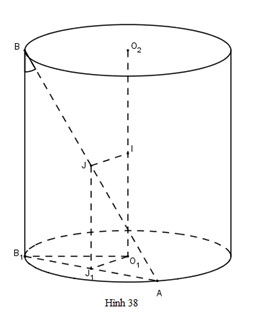
c) Giả sử trục của hình trụ là \(O_1O_2\) và \(A\) nằm trên đường tròn tâm \(O_1\), \(B\) nằm trên đường tròn tâm \(O_2\); \(I\) là trung điểm của \(O_1O_2\) , \(J\) là trung điểm của \(AB\). Khi đó \(IJ\) là đường vuông góc chung của \(O_1O_2\) và \(AB\). Hạ \(BB_1\) vuông góc với đáy, \(J_1\) là hình chiếu vuông góc của \(J\) xuống đáy.
Ta có \( J_{1}\) là trung điểm của \( AB_{1}\), \( O_{1}J_{1}\) = \(IJ\).
Theo giả thiết \( \widehat{B_{1}BA}\) = \(30^0\).
do vậy: \(AB_1 = BB_1.tan 30^0\) = \( \frac{\sqrt{3}}{3}h = r\).
Xét tam giác vuông \(O_1J_1A\) vuông tại \(J_1\) ta có:
\( O_{1}J^{2}_{1}\) = \( O_{1}A^{2}\) - \( AJ^{2}_{1} =\) \( r^{2} - {\left( {{r \over 2}} \right)^2}=\) \( \frac{3}{4}r^{2}\).
Vậy khoảng cách giữa \(AB\) và \(O_1O_2\) là: \( \frac{\sqrt{3}}{2}r\)
