
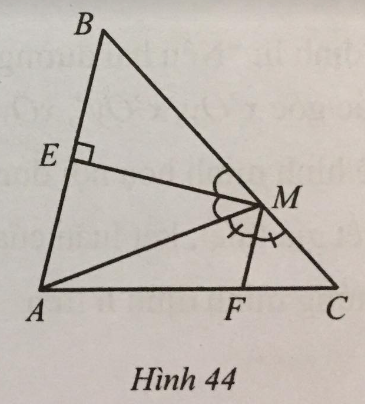
Quan sát Hình 44, biết ME vuông góc với AB tại E và ME, MF lần lượt là tia phân giác của góc AMB và AMC. Vì sao hai đường thẳng MF và AB song song với nhau?

Chứng minh hai đường thẳng song song bằng cách chứng minh hai góc bằng nhau và chúng ở một trong các vị trí: đồng vị, so le trong, so le ngoài.
Advertisements (Quảng cáo)

Do hai góc AME và AMF là hai góc kề nhau nên \(\widehat {EMF} = \widehat {AME} + \widehat {AMF}\).
Ta có ME, MF lần lượt là tia phân giác của góc AMB và AMC nên
\(\widehat {AME} = \dfrac{1}{2}\widehat {AMB};{\rm{ }}\widehat {AMF} = \dfrac{1}{2}\widehat {AMC}\).
Mà \(\widehat {AMB} + \widehat {AMC} = 180^\circ \) (hai góc kề bù) nên
\(\widehat {EMF} = \widehat {AME} + \widehat {AMF} = \dfrac{1}{2}\left( {\widehat {AMB} + \widehat {AMC}} \right) = \dfrac{1}{2}{\rm{ }}{\rm{. 180}}^\circ {\rm{ = 90}}^\circ \).
Suy ra: \(\widehat {EMF} = \widehat {MEB}\) mà hai góc này ở vị trí so le trong nên MF // AB (Dấu hiệu nhận biết 2 đường thẳng song song)
