
Nêu thêm một điều kiện để hai tam giác trong mỗi hình 31a, 31b, 31c, 31d là hai tam giác bằng nhau theo trường hợp góc – cạnh – góc.
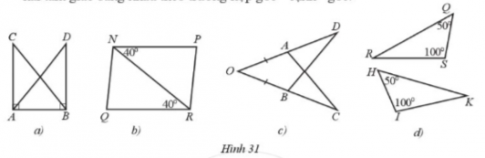
a) ∆CAB = ∆DBA (Hình 31a).
b) ∆NRQ = ∆RNP (Hình 31b).
c) ∆OAC = ∆OBD (Hình 31c).
d) ∆SRQ = ∆IKH (Hình 31d).

Quan sát các hình để thêm các điều biện bằng nhau của tam giác theo trường hợp goc – cạnh – góc

a) Hình a
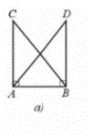
Để ∆CAB = ∆DBA theo trường hợp góc – cạnh – góc thì một cạnh và hai góc kề của tam giác này bằng một cạnh và hai góc kề của tam giác kia.
Mà hai tam giác trên có cạnh AB là cạnh chung và \(\widehat {CAB} = \widehat {DBA}\left( { = 90^\circ } \right)\).
Mặt khác, trong ∆CAB thì cạnh AB có hai góc kề là \(\widehat {CAB}\) và \(\widehat {ABC}\);
Trong ∆DBA thì cạnh AB có hai góc kề là \(\widehat {DBA}\) và \(\widehat {BAD}\) .
Do đó điều kiện còn lại là điều kiện về góc, đó là \(\widehat {ABC} = \widehat {BAD}\)
Vậy Hình 31a cần thêm điều kiện \(\widehat {ABC} = \widehat {BAD}\) .
b) Hình b
Advertisements (Quảng cáo)
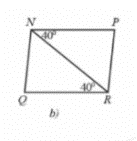
Để ∆NRQ = ∆RNP theo trường hợp góc – cạnh – góc thì một cạnh và hai góc kề của tam giác này bằng một cạnh và hai góc kề của tam giác kia.
Mà hai tam giác trên có cạnh NR là cạnh chung và \(\widehat {PN{\rm{R}}} = \widehat {{\rm{QRN}}}\left( { = 40^\circ } \right)\).
Mặt khác, trong ∆NRQ, cạnh NR có hai góc kề là \(\widehat {PNR}\) và \(\widehat {PRN}\) ;
Trong ∆RNP, cạnh NR có hai góc kề là \(\widehat {QRN}\) và \(\widehat {QNR}\)
Do đó điều kiện còn lại là điều kiện về góc, đó là \(\widehat {PRN} = \widehat {QNR}.\)
Vậy Hình 31b cần thêm điều kiện \(\widehat {PRN} = \widehat {QNR}.\).
c) Hình c
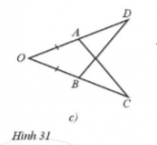
Để ∆OAC = ∆OBD theo trường hợp góc – cạnh – góc thì một cạnh và hai góc kề của tam giác này bằng một cạnh và hai góc kề của tam giác kia.
Mà hai tam giác trên có OA = OB và \(\hat O\) là góc chung.
Mặt khác, trong ∆OAC, cạnh OA có hai góc kề là \(\hat O\) và \(\widehat {OAC}\);
Trong ∆OBD, cạnh OB có hai góc kề là \(\hat O\) và \(\widehat {OBD}\) .
Do đó điều kiện còn lại là điều kiện về góc, đó là \(\widehat {OAC} = \widehat {OBD}\).
Vậy Hình 31c cần thêm điều kiện \(\widehat {OAC} = \widehat {OBD}\).
d) Hình d

Để ∆SRQ = ∆IKH theo trường hợp góc – cạnh – góc thì một cạnh và hai góc kề của tam giác này bằng một cạnh và hai góc kề của tam giác kia.
Mà hai tam giác này có \(\hat Q = \hat H\left( { = 50^\circ } \right)\) và \(\hat S = \hat I\left( { = 100^\circ } \right)\)
Mặt khác, trong ∆SRQ, \(\hat Q\) và \(\hat S\) là hai góc kề của cạnh QS;
Trong ∆IKH, \(\hat H\) và \(\hat I\) là hai góc kề của cạnh HI.
Do đó điều kiện còn lại là điều kiện về cạnh, đó là QS = HI.
Vậy Hình 31d cần thêm điều kiện QS = HI.
