Giải Bài 38 trang 81 sách bài tập toán 7 – Cánh diều – Bài 6: Trường hợp bằng nhau thứ ba của tam giác: góc-cạnh-góc
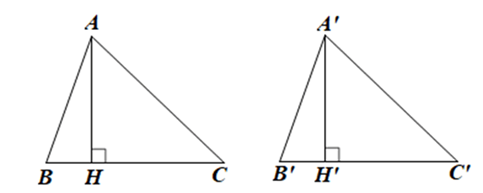
Cho ∆ABC = ∆A’B’C’. Vẽ AH vuông góc với BC tại H, A’H’ vuông góc với B’C’ tại H’. Chứng minh AH = A’H’.
– Chứng minh: \(\Delta ABH = \Delta A’B’H’\) (cạnh huyền – góc nhọn)
– Suy ra: AH = A’H’.
Do ∆ABC = ∆A’B’C’ (giả thiết)
Nên AB = A’B’ (hai cạnh tương ứng) và (hai góc tương ứng).
Advertisements (Quảng cáo)
Xét ∆ABH và ∆AB’H’ có:
\(\widehat {AHB} = \widehat {A’H’B’}\left( { = 90^\circ } \right)\)
AB = A’B’ (chứng minh trên),
\(\widehat {ABH} = \widehat {A’B’H’}\) (do \(\widehat {ABC} = \widehat {A’B’C’}\))
Suy ra ∆ABH = ∆A’B’H’ (cạnh huyền – góc nhọn).
Do đó AH = A’H’ (hai cạnh tương ứng).
Vậy AH = A’H’.