
Quan sát Hình 49. Chứng tỏ:
a) yy’ // zz’; b) \(ut \bot zz’\); c) xx’ // zz’.
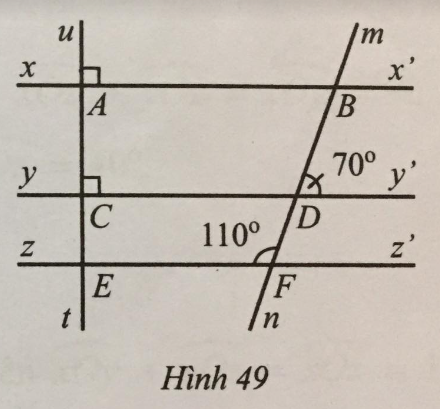

a) Chứng minh yy’ // zz’ bằng cách chứng minh 1 đường thẳng cắt yy’ và zz’ tạo ra cặp góc đồng vị bằng nhau
Advertisements (Quảng cáo)
b) Chứng minh \(ut \bot zz’\) dựa vào yy’ // zz’ và \(ut \bot yy’\).
c) Dấu hiệu nhận biết 2 đường thẳng song song

a) Ta có \(\widehat {DFE} + \widehat {DFz’} = 180^\circ \) (hai góc kề bù) nên \(\widehat {DFz’} = 180^\circ - \widehat {DFE} = 180^\circ - 110^\circ = 70^\circ \).
Do đó \(\widehat {DFz’} = \widehat {BDy’}\) mà hai góc này ở vị trí đồng vị nên yy’ // zz’.
b) Do yy’ // zz’ nên \(\widehat {uEz’} = \widehat {uCy’} = 90^\circ \Rightarrow ut \bot zz’\).
c) Ta có \(\widehat {uAx’} = \widehat {uEz’} = 90^\circ \) và chúng ở vị trí đồng vị nên xx’ // zz’ (Dấu hiệu nhận biết 2 đường thẳng song song)
