
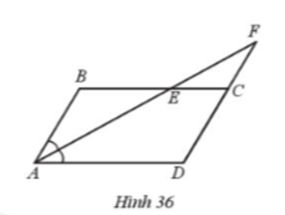
Ở Hình 36 có AB song song cới CD, BC song song với AD. Tia phân giác của góc BAD cắt BC tại E và cắt tia DC tại F.
a) Chứng minh các tam giác ABE, CEF, DAF là các tam giác cân.
b) Tính số đo mỗi góc của tam giác ADF, biết \(\widehat {BAD} = 60^\circ \)

- Chứng minh hai goác ở đáy bằng nhau suy ra tam giác cân
- Vì AB // CD nên \(\widehat {BA{\rm{D}}} + \widehat {A{\rm{D}}F} = {180^o}\) và tổng ba góc trong một tam giác để tính ra số đo của mỗi góc cần tìm.

a) • Vì AE là tia phân giác của \(\widehat {BAD}\) nên \(\widehat {BAE} = \widehat {EAD}\).
Vì BC // AD nên \(\widehat {BEA} = \widehat {EAD}\) (hai góc so le trong)
Do đó \(\widehat {BAE} = \widehat {BEA}\).
Advertisements (Quảng cáo)
Suy ra tam giác ABE cân tại B.
• Vì AB // CD nên \(\widehat {BAE} = \hat F\) (hai góc so le trong).
Mà \(\widehat {BAE} = \widehat {BEA}\) chứng minh trên), \(\widehat {CEF} = \widehat {BEA}\) (hai góc đối đỉnh).
Suy ra \(\widehat {CEF} = \hat F\)
Nên tam giác CEF cân tại C.
• Ta có \(\widehat {BAF} = \widehat {{\rm{DAF}}}\) và \(\widehat {BAF} = \widehat {DFA}\) nên \(\widehat {DAF} = \widehat {DFA}\)
Do đó tam giác DAF cân tại D.
Vậy ∆ABE cân tại B, ∆CEF cân tại C, ∆DAF cân tại D.
b) Vì AB // CD nên \(\widehat {BAD} + \widehat {ADF} = 180^\circ \) (hai góc trong cùng phía)
Suy ra \(\widehat {ADF} = 180^\circ - \widehat {BAD} = 180^\circ - 60^\circ = 120^\circ \)
Xét ∆ADF có \(\widehat {ADF} + \widehat {DFA} + \widehat {DAF} = 180^\circ \) (tổng ba góc của một tam giác).
Mà \(\widehat {ADF} = 120^\circ \), \(\widehat {DAF} = \widehat {DFA}\)
Nên \(\widehat {DAF} = \widehat {DFA} = \frac{{180^\circ - \widehat {ADF}}}{2} = \frac{{180^\circ - 120^\circ }}{2} = 30^\circ \)
Vậy \(\widehat {DAF} = \widehat {DFA} = 30^\circ ,\widehat {FDA} = 120^\circ .\)
