
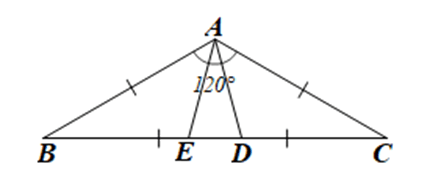
Cho tam giác ABC cân tại A có \(\widehat {BAC} = 120^\circ \) Trên cạnh BC lấy các điểm D, E sao cho BD = BA, CE = CA.
a) Chứng minh các tam giác BAD, CAE, AED là các tam giác cân.
b) Tính số đo mỗi góc của tam giác ADE.

- BD = BA suy ra tam giác ABD cân tại B.
- CA = CE suy ra tam giác ACE cân tại C.
- Chứng minh: \(\widehat {A{\rm{D}}E} = \widehat {A{\rm{ED}}}\) suy ra tam giác AED cân tại A.
- Tổng ba góc trog một tam giác bằng \({180^o}\) để tính số đo mỗi góc của tam giác ADE.

a) Vì BD = BA (giả thiết) nên tam giác ABD cân tại B.
Suy ra \(\widehat {BAD} = \widehat {BDA}\) (hai góc ở đáy).
Vì CE = CA (giả thiết) nên tam giác ACE cân tại C.
Suy ra \(\widehat {CAE} = \widehat {CEA}\) (hai góc ở đáy).
Advertisements (Quảng cáo)
Vì tam giác ABC cân tại A nên \(\widehat {ABC} = \widehat {ACB}\)
• Xét ∆ABC có: \(\widehat {BAC} + \widehat {CBA} + \widehat {BCA} = 180^\circ \) (tổng ba góc của một tam giác)
Mà \(\widehat {BAC} = 120^\circ \) (giả thiết), \(\widehat {ABC} = \widehat {ACB}\)
Suy ra \(\widehat {ABC} = \widehat {ACB} = \frac{{180^\circ - \widehat {BAC}}}{2} = \frac{{180^\circ - 120^\circ }}{2} = 30^\circ \)
• Xét ∆ABD có: \(\widehat {BAD} + \widehat {DBA} + \widehat {BDA} = 180^\circ \) (tổng ba góc của một tam giác)
Mà \(\widehat {BAD} = \widehat {BDA}\), \(\widehat {BAD} = \widehat {BDA}\)
Suy ra \(\widehat {ADB} = \frac{{180^\circ - \widehat {ABD}}}{2} = \frac{{180^\circ - 30^\circ }}{2} = 75^\circ \)
• Xét ∆ACE có: \(\widehat {ACE} + \widehat {AEC} + \widehat {CAE} = 180^\circ \) (tổng ba góc của một tam giác)
Mà \(\widehat {CAE} = \widehat {CEA}\), \(\widehat {CAE} = \widehat {CEA}\)
Suy ra \(\widehat {AEC} = \frac{{180^\circ - \widehat {ACE}}}{2} = \frac{{180^\circ - 30^\circ }}{2} = 75^\circ \).
Xét tam giác ADE có \(\widehat {ADE} = \widehat {AED}\) (cùng bằng 75°).
Suy ra tam giác AED cân tại A.
Vậy ∆ABD cân tại B, ∆ACE cân tại C và ∆AED cân tại A.
b) Xét ∆ADE có: \(\widehat {ADE} + \widehat {AED} + \widehat {DAE} = 180^\circ \) (tổng ba góc của một tam giác)
Suy ra \(\widehat {DAE} = 180^\circ - \widehat {ADE} - \widehat {AED} = 180^\circ - 75^\circ - 75^\circ = 30^\circ \)
Vậy ∆ADE có \(\widehat {ADE} = \widehat {AED} = 75^\circ ,\widehat {EAD} = 30^\circ .\)
