Cho tam giác ABC. Các tia phân giác của các góc B và C cắt nhau ở I. Tính \(\widehat {BIC}\) biết rằng:
a) \({\rm{}}\widehat B = 80^\circ ,\widehat C = 40^\circ \)
b) \(\widehat A = 80^\circ \)
c) \(\widehat A = m^\circ \)

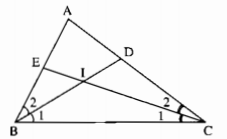
a) Ta có
\(\widehat {{B_1}} = {1 \over 2}\widehat {ABC} = {1 \over 2}.80^\circ = 40^\circ \) (vì BD là tia phân giác của \(\widehat {ABC}\))
\(\widehat {{C_1}} = {1 \over 2}\widehat {ACB} = {1 \over 2}.40^\circ = 20^\circ \) (vì CE là tia phân giác của \(\widehat {ACB}\))
Trong ∆IBC, ta có: \(\widehat {BIC} + \widehat {{B_1}} + \widehat {{C_1}} = 180^\circ \) (tổng 3 góc trong tam giác)
\(\widehat {BIC} = 180^\circ - \left( {\widehat {\widehat {{B_1}} + {C_1}}} \right) = 180^\circ - \left( {40^\circ + 20^\circ } \right) = 120^\circ \)
Advertisements (Quảng cáo)
b) Ta có:
\(\widehat {{B_1}} = {1 \over 2}\widehat B\) (vì BD là tia phân giác \(\widehat B\))
\(\widehat {{C_1}} = {1 \over 2}\widehat C\) (vì CE là tia phân giác \(\widehat C\))
Trong ∆ABC, ta có:
\(\widehat A + \widehat B + \widehat C = 180^\circ \) (tổng ba góc trong tam giác)
Suy ra \(\widehat B + \widehat C = 180^\circ - \widehat A = 180^\circ - 80^\circ = 100^\circ \)
Trong ∆IBC, ta có: \(\widehat {BIC} + \widehat {{B_1}} + \widehat {{C_1}} = 180^\circ \)
Vậy \(\widehat {BIC} = 180^\circ - \left( {\widehat {{B_1}} + \widehat {{C_1}}} \right) = 180^\circ - {{\widehat B + \widehat C} \over 2} = 180^\circ - {{100^\circ } \over 2} = 130^\circ \)
c) Ta có: \(\widehat B + \widehat C = 180 - m^\circ \)
Vậy \(\widehat {BIC} = 180^\circ - {{180^\circ - m^\circ } \over 2} = 180^\circ - 90^\circ + {{m^\circ } \over 2} = 90^\circ + {{m^\circ } \over 2}\)
