Chứng minh rằng nếu một đường thẳng cắt hai đường thẳng song song thì hai tia phân giác của cặp góc trong cùng phía vuông góc với nhau.

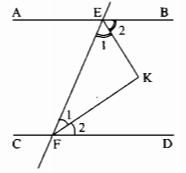
Giả sử đường thẳng AB // CD cắt đường thẳng EF tại E và F
Ta có: \(\widehat {BEF} + \widehat {EFD} = 180^\circ \) (hai góc trong cùng phía)
Advertisements (Quảng cáo)
\(\eqalign{
& \widehat {{E_1}} = {1 \over 2}\widehat {{\rm{BEF}}}\left( {gt} \right) \cr
& \widehat {{F_1}} = {1 \over 2}\widehat {EFD}\left( {gt} \right) \cr} \)
\( \Rightarrow \widehat {{E_1}} + \widehat {{F_1}} = {1 \over 2}\left( {\widehat {{\rm{BEF}}} + \widehat {EFD}} \right) = 90^\circ \)
Trong ∆EKF, ta có:
\(\widehat {EKF} = 180^\circ - \left( {\widehat {{E_1} + \widehat {{F_1}}}} \right) = 180^\circ - 90^\circ = 90^\circ \)
Vậy \(EK \bot FK\).
