Gọi G là trọng tâm của tam giác ABC. Vẽ điểm D sao cho G là trung điểm của AD. Chứng minh rằng:
a) Các cạnh của tam giác BGD bằng \({2 \over 3}\) các đường trung tuyến của tam giác ABC
b) Các đường trung tuyến của tam giác BGD bằng một nửa các cạnh của tam giác ABC.

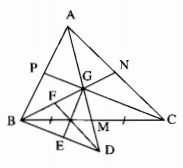
a) Gọi AM, BN, CP là các đường trung tuyến của ∆ABC cắt nhau tại G.
AG = GD (gt)
AG = 2GM (suy ra từ tính chất đường trung tuyến)
Nên GD = 2GM
GD = GM + MD
Suy ra: GM = MD
Xét ∆BMD và ∆CMG:
BM = CM (gt)
\(\widehat {BM{\rm{D}}} = \widehat {CMG}\) (đối đỉnh)
MD = GM (chứng minh trên)
Do đó: ∆BMD = ∆CMG (c.g.c)
\( \Rightarrow \) BD = CG
\(CG = {2 \over 3}CP\) (tính chất đường trung tuyến)
Suy ra: \(B{\rm{D = }}{2 \over 3}CP\) (1)
\(BG = {2 \over 3}BN\) (tính chất đường trung tuyến) (2)
\({\rm{A}}G = {2 \over 3}AM\) (tính chất đường trung tuyến)
Suy ra: \(G{\rm{D}} = {2 \over 3}AM\) (3)
Từ (1), (2) và (3) suy ra các cạnh của ∆BGD bằng \({2 \over 3}\) các đường trung tuyến của ∆ABC.
b) GM = MD (chứng minh trên)
nên BM = MD là đường trung tuyến của ∆BGD
Advertisements (Quảng cáo)
\(BM = {1 \over 2}BC\) (4)
Kẻ đường trung tuyến GE và DF của ∆BGD
\( \Rightarrow FG = {1 \over 2}BG\)
\(GN = {1 \over 2}BG\) (tính chất đường trung tuyến)
Nên FN = GN
Xét ∆DFG và ∆ANG:
AG = GD (gt)
\(\widehat {DGF} = \widehat {AGN}\) (đối đỉnh)
GF = GN (chứng minh trên)
Do đó ∆DFG = ∆ANG (c.g.c)
\( \Rightarrow \) DF = AN
\(AN = {1 \over 2}AC\) (gt)
Suy ra: \({\rm{D}}F = {1 \over 2}AC\) (5)
BD = CG (chứng minh trên)
\({\rm{ED}} = {1 \over 2}B{\rm{D}}\) (Vì E là trung điểm BD)
\(GP = {1 \over 2}CG\) (tính chất đường trung tuyến)
Suy ra: ED = GP
∆BDM = ∆CGM (chứng minh trên)
\( \Rightarrow \widehat {B{\rm{D}}M} = \widehat {CGM}\) hay \(\widehat {E{\rm{D}}G} = \widehat {CGM}\)
\(\widehat {CGM} = \widehat {PGA}\) (đối đỉnh)
Suy ra: \(\widehat {{\rm{ED}}G} = \widehat {PGA}\)
AG = GD (gt)
Suy ra: ∆PGA = ∆EDG (c.g.c)=> GE = AP mà
Suy ra: \(GE = {1 \over 2}AB\) (6)
Từ (4),(5) và (6) suy ra các đường trung tuyến của ∆BGD bằng một nửa cạnh của ∆ABC.
