Chứng minh rằng BD + CE < 15cm.. Câu 35 trang 42 Sách Bài Tập (SBT) Toán lớp 7 tập 2 - Bài 4: Tính chất ba đường trung tuyến của tam giác
Tam giác ABC có BC = 10cm, các đường trung tuyến BD và CE. Chứng minh rằng BD + CE < 15cm.

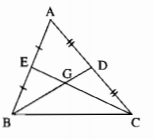
Gọi G là giao điểm của 2 đường trung tuyến BD và CE.
Trong ∆GBC ta có:
GB + GC > BC (bất đẳng thức tam giác)
Advertisements (Quảng cáo)
\(GB = {2 \over 3}B{\rm{D}}\) (tính chất đường trung tuyến)
\(GC = {2 \over 3}CE\) (tính chất đường trung tuyến)
BC = 10cm (gt)
Suy ra: \({2 \over 3}\left( {B{\rm{D}} + CE} \right) > 10 \)
\(\Rightarrow B{\rm{D}} + CE > 10:{2 \over 3} = 10.{3 \over 2} = 15\)
Vây BD + CE > 15 (cm)
