Với hai góc kề bù, ta có định lí sau:
Hai tia phân giác của hai góc kề bù tạo thành một góc vuông.
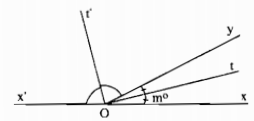
a) Hãy vẽ hai góc xOy và y’Ox kề bù, tia phân giác Ot của góc xOy, tia phân giác Ot’ của góc yOx’ và gọi số đo của góc xOy là m°.
b) Hãy viết giả thiết và kết luận của định lí.
c) Hãy điền vào chỗ trống (…) và sắp xếp bốn câu sau đây một cách hợp lý để chứng minh định lí trên:
\(1.\widehat {tOy} = {1 \over 2}m^\circ \) vì ……..
\(2.\widehat {t’Oy} = {1 \over 2}(180^\circ - m^\circ )\) vì …….
\(3.\widehat {tOt’} = 90^\circ \) vì ……
\(4.\widehat {x’Oy} = 180^\circ - m^\circ \) vì …….
Advertisements (Quảng cáo)

a) Hình vẽ:
b)
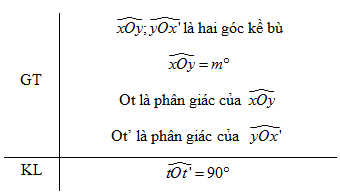
c) \(\widehat {x’Oy} = 180^\circ - m^\circ \) (Vì \(\widehat {x’Oy}\) và \(\widehat {{\rm{yOx}}}\) kề bù)
\(\widehat {tOy} = {1 \over 2}m^\circ \) (Vì Ot là tia phân giác của \(\widehat {x’Oy}\))
\(\widehat {t’Oy} = {1 \over 2}\left( {180^\circ - m^\circ } \right)\) (Vì Ot’ là tia phân giác của \(\widehat {yOx’}\))
\(\widehat {tOt’} = 90^\circ \) (Vì Oy nằm giữa Ot và Ot’)
