Cho tam giác ABC. Hãy tìm một điểm sao cho khoảng cách từ điểm đó đến mỗi đoạn thẳng AB, BC, CA là bằng nhau, đồng thời khoảng cách này là ngắn nhất.

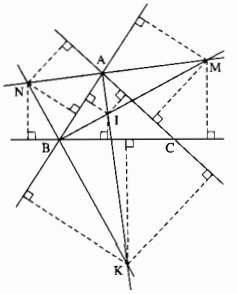
Nếu O là điểm nằm trong ∆ABC
Kẻ \(OH \bot AB,OK \bot BC,OI \bot {\rm{A}}C\)
Vì điểm O cách đều các đường thẳng AB, BC, CA.
\( \Rightarrow \) OH = OK = OI
OH = OK
\( \Rightarrow \) O nằm trên tia phân giác \(\widehat {ABC}\)
OI = OK
\( \Rightarrow \) O nằm trên tia phân giác \(\widehat {ACB}\)
Advertisements (Quảng cáo)
Vậy O là giao điểm các đường phân giác của ∆ABC.
Nếu O’ nằm ngoài ∆ABC
Kẻ \(O’D \bot AB,O’E \bot BC,O’F \bot {\rm{AC}}\)
\( \Rightarrow \) O’D = O’E = O’F
O’D = O’F
\( \Rightarrow \) O nằm trên tia phân giác \(\widehat {BAC}\)
O’D = O’E
\( \Rightarrow \) O’ nằm trên tia phân giác \(\widehat {DBC}\)
\( \Rightarrow \) O’ là giao điểm phân giác trong của \(\widehat {BAC}\) và phân giác ngoài tại đỉnh D. nên A, O, O’ thẳng; A, H, D thẳng hàng.
Ta có: OH < O’D
Vậy O là giao điểm các đường phân giác trong của ∆ABC cách đều ba đường thẳng AB, BC, CA và ngắn nhất.
