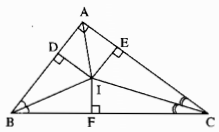
Cho tam giác ABC vuông tại A. Các tia phân giác của các góc B và C cắt nhau tại I. Gọi D và E là chân các đường vuông góc kẻ từ I đến AB và AC.
a) Chứng minh rằng AD = AE.
b) Tính các dộ dài AD, AE biết rằng AB = 6cm, AC = 8cm.

a) I là giao điểm phân giác trong của \(\widehat B\) và \(\widehat C\) nên AI là tia phân giác của Â.
\( \Rightarrow \) ID = IE (tính chất tia phân giác) (1)
∆ADI vuông tại D có \(\widehat {DAI} = 45^\circ \)
Nên ∆ADI vuông cân tại D.
\( \Rightarrow \) ID = DA (2)
∆AEI vuông tại E có \(\widehat {E{\rm{A}}I} = 45^\circ \)
Nên ∆ AEI vuông cân tại E
\( \Rightarrow \) IE = AE (3)
Từ (1), (2) và (3) suy ra: AD = AE
b) Trong tam giác vuông ABC có Â=90°
Theo định lý Pitago ta có:
\(\eqalign{
& B{C^2} = A{B^2} + A{C^2} \cr
& B{C^2} = {6^2} + {8^2} = 36 + 64 = 100 \cr} \)
\( \Rightarrow \) BC = 10 (cm)
Advertisements (Quảng cáo)
Kẻ \(IF \bot BC\)
Xét hai tam giác vuông IDB và IFB:
\(\eqalign{
& \widehat {IDB} = \widehat {IFB} = 90^\circ \cr
& \widehat {DBI} = \widehat {FBI}\left( {gt} \right) \cr} \)
Cạnh huyền BI chung
Do đó: ∆IDB = ∆IFB (cạnh huyền, góc nhọn)
\( \Rightarrow \) DB = FB (4)
Xét hai tam giác vuông IEC và IFC:
\(\eqalign{
& \widehat {IEC} = \widehat {IFC} = 90^\circ \cr
& \widehat {ECI} = \widehat {FCI}\left( {gt} \right) \cr} \)
Cạnh huyền CI chung
Do đó: ∆IEC = ∆IFC (cạnh huyền, góc nhọn)
\( \Rightarrow \) CE = CF (5)
AD + AE = AB – DB + AC – CE
\( \Rightarrow \) AD + AE = AB + AC – (DB + CF) (6)
Từ (4), (5) và (6) suy ra:
AD + AE = AB + AC – (FB + FC) = AB + AC – BC
AD + AE = 6 + 8 – 10 = 4 (cm)
Mà AD = AE (chứng minh trên)
\( \Rightarrow \) AD = AE = 4: 2 = 2 (cm)
