Cho tam giác ABC. Các tia phân giác các góc A và C cắt nhau ở I. Các đường phân giác các góc ngoài tại đỉnh A và C cắt nhau ở K. Chứng minh rằng ba điểm B, I, K thẳng hàng.

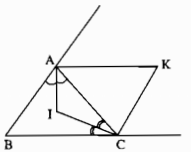
Kẻ \(IH \bot AB,IJ \bot BC,IG \bot AC\),
\(KD \bot AB,KE \bot AC,KF \bot BC\)
I nằm trên tia phân giác của \(\widehat {BAC}\)
\( \Rightarrow \) IH = IG (tính chất tia phân giác)
I nằm trên tia phân giác của \(\widehat {BCA}\)
\( \Rightarrow \) IG = IJ (tính chất tia phân giác)
Advertisements (Quảng cáo)
Suy ra: IH = IJ
Nên I nằm trên tia phân giác của \(\widehat {ABC}\) (1)
K nằm trên tia phân giác của \(\widehat {DAC}\)
\( \Rightarrow \) KD = KE (tính chất tia phân giác)
K nằm trên tia phân giác của \(\widehat {ACF}\)
\( \Rightarrow \) KE = KF (tính chất tia phân giác)
Suy ra: KD = KF => K nằm trên tia phân giác của \(\widehat {ABC}\) (2)
Từ (1) và (2) suy ra: B, I, K thẳng hàng
