Tính góc A của tam giác ABC biết rằng các đường phân giác BD, CB cắt nhau tại I trong đó góc BIG bằng:
a) 120°
b) ∝(∝ > 90°)

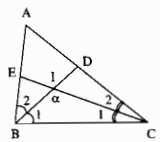
Trong ∆BIC ta có: \(\widehat {BIC} + \widehat {{B_1}} + \widehat {{C_1}} = 180^\circ \) (tổng 3 góc trong tam giác)
Advertisements (Quảng cáo)
\(\Rightarrow \widehat {{B_1}} + \widehat {{C_1}} = 180^\circ - \widehat {BIC} = 180^\circ - 120^\circ = 60^\circ \)
\(\widehat {{B_1}} = {1 \over 2}\widehat B\) (Vì BD là tia phân giác)
\(\widehat {{C_1}} = {1 \over 2}\widehat C\) (Vì CE là tia phân giác)
\( \Rightarrow \widehat B + \widehat C = 2\left( {\widehat {{B_1}} + \widehat {{C_1}}} \right) = 2.60^\circ = 120^\circ \)
Trong ∆ABC ta có: \(\widehat A + \widehat B + \widehat C = 180^\circ \) (tổng ba góc trong tam giác)
\( \Rightarrow \widehat A = 180^\circ - (\widehat B + \widehat C) = 180^\circ - 120^\circ = 60^\circ \)
