Hãy chứng tỏ Am // BC.. Câu 6 trang 137 Sách Bài Tập (SBT) Toán lớp 7 tập 1 - Bài 1: Tổng ba góc của một tam giác
Cho tam giác ABC có \(\widehat B = \widehat C = 50^\circ \). Gọi tia Am là tia phân giác của góc ngoài ở đỉnh A. Hãy chứng tỏ Am // BC
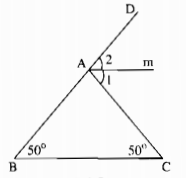
Trong ∆ABC, ta có: \(\widehat {CA{\rm{D}}}\) là góc ngoài tại đỉnh A
Advertisements (Quảng cáo)
\(\widehat {CAD}{\rm{ = }}\widehat B + \widehat C = 50^\circ + 50^\circ = 100^\circ \) (tính chất góc ngoài của tam giác)
\(\widehat {{A_1}} = \widehat {{A_2}} = {1 \over 2}\widehat {CA{\rm{D}}} = 50^\circ \) (Vì tia Am là tia phân giác của \(\widehat {CA{\rm{D}}}\))
Suy ra: \(\widehat {{A_1}} = \widehat C = 50^\circ \)
\( \Rightarrow \) Am // BC (Vì có cặp góc ở vị trí so le trong bằng nhau)