Tam giác ABC có M là trung điểm của BC và AM là tia phân giác của góc A. Chứng minh rằng tam giác ABC là tam giác cân.

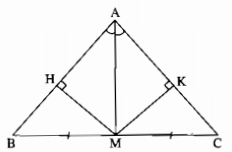
Kẻ \(MH \bot AB,MK \bot AC\)
Xét hai tam giác vuông AHM và AKM, ta có:
\(\eqalign{
& \widehat {AHM} = \widehat {AKM} = 90^\circ \cr
& \widehat {HAM} = \widehat {K{\rm{A}}M\left( {gt} \right)} \cr} \)
AM cạnh huyền chung
\( \Rightarrow \) ∆AHM = ∆AKM (cạnh huyền, góc nhọn)
Advertisements (Quảng cáo)
Suy ra: MH = MK (hai cạnh tương ứng)
Xét hai tam giác vuông MHB và MKC, ta có:
\(\widehat {MHB} = \widehat {MKC} = 90^\circ \)
MH = MK (chứng minh trên)
MB = MC (gt)
Suy ra: ∆MHB = ∆MKC (cạnh huyền, cạnh góc vuông)
Suy ra: \(\widehat B = \widehat C\) (hai góc tương ứng)
Vậy ∆ABC cân tại A.
