Chứng minh rằng AI là tia phân giác của góc A.. Câu 96 trang 151 Sách Bài Tập (SBT) Toán lớp 7 tập 1 - Bài 8: Các trường hợp bằng nhau của tam giác vuông
Cho tam giác ABC cân tại A. Các đường trung trực của AB, AC cắt nhau ở I. Chứng minh rằng AI là tia phân giác của góc A.
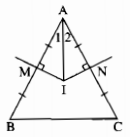
Ta có:
\(\eqalign{
& AB{\rm{ }} = {\rm{ }}AC\left( {gt} \right){\rm{ }}\left( 1 \right); \cr
& {\rm{ }}AM{\rm{ }} = {1 \over 2}AB\left( {gt} \right)\left( 2 \right); \cr
& AN = {1 \over 2}AC\left( {gt} \right)\left( 3 \right) \cr} \)
Từ (1), (2) và (3) suy ra: AM = AN
Xét hai tam giác vuông AMI và ANI, ta có:
Advertisements (Quảng cáo)
\(\widehat {AMI} = \widehat {ANI} = 90^\circ \)
AM = AN (chứng minh trên)
AI cạnh huyền chung
Suy ra: ∆AMI = ∆ANI (cạnh huyền, cạnh góc vuông)
Suy ra \(\widehat {{A_1}} = \widehat {{A_2}}\) (hai góc tương ứng)
Vậy AI là tia phân giác của \(\widehat {BAC}\).