
Cho tam giác ABC vuông tại A. Tia phân giác của góc C cắt AB ở M. Từ B kẻ BH vuông góc với đường thẳng CM \(\left( {H \in CM} \right)\). Trên tia đối của tia HC lấy điểm E sao cho HE = HM.
a) Chứng minh rằng tam giác MBE cân.
b) Chứng minh rằng \(\widehat {EBH} = \widehat {ACM}\)
c) Chứng minh rằng \(EB \bot BC\)
d) Đường thẳng BE cắt đường thẳng AC tại N. Tia phân giác \(\widehat {NAB}\) cắt đường thẳng BH tại D, tia ND cắt CM tại F. Tính số đo \(\widehat {NFC}\)

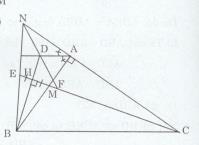
a) ∆MBE có: BH là đường cao (\(BH \bot EM\) tại H)
BH là đường trung tuyến (HE = HM, \(H \in EM\))
Nên ∆MBE cân tại B.
b) ∆MBE cân tại B có BH là đường cao
=> BH cũng là đường phân giác \( \Rightarrow \widehat {EBH} = \widehat {HBM}\)
Ta có: \(\widehat {HBM} + \widehat {BMH} = 90^\circ\) (∆HMB vuông tại H)
\(\widehat {ACM} + \widehat {AMC} = 90^\circ\) (∆AMC vuông tại A)
\(\widehat {BMH} = \widehat {AMC}\) (đối đỉnh)
Do đó \(\widehat {HBM} = \widehat {ACM}.\)
Mà \(\widehat {HBM} = \widehat {EBH}.\)
Advertisements (Quảng cáo)
Nên \(\widehat {ACM} = \widehat {EBH}.\)
c) Ta có: \(\widehat {EBH} = {1 \over 2}\widehat {EBM}\) (BH là tia phân giác của \(\widehat {EBM}\))
\(\widehat {ACM} = {1 \over 2}\widehat {ACB}\) (CM là tia phân giác của \(\widehat {ACB}\))
\(\widehat {EBH} = \widehat {ACM}\) (câu b)
Do đó \(\widehat {EBM} = \widehat {ACB}.\)
Mà \(\widehat {ACB} + \widehat {MBC} = 90^\circ\) (∆ABC vuông tại A). Nên \(\widehat {EBM} + \widehat {MBC} = 90^\circ\).
\( \Rightarrow \widehat {EBC} = 90^\circ\). Vậy\(EB \bot BC.\)
d) ∆ABN có: AD là đường phân giác (gt)
BD là đường phân giác và AD cắt BD tại D (gt)
=> D là giao điểm ba đường phân giác của tam giác ABN
=> ND là đường phân giác của ∆ABN \( \Rightarrow \widehat {ANF} = {1 \over 2}\widehat {BNC}\)
Mà \(\widehat {NCF} = {1 \over 2}\widehat {NCB}\) (CF là tia phân giác của \(\widehat {NCB}\))
\(\widehat {BNC} + \widehat {NCB} = 90^\circ\) (∆NBC vuông tại B)
Nên \(\widehat {ANF} + \widehat {NCF} = {1 \over 2}\widehat {BNC} + {1 \over 2}\widehat {NCB} = {1 \over 2}(\widehat {BNC} + \widehat {NCB}) = {1 \over 2}.90^\circ = 45^\circ .\)
Lại có \(\widehat {NFC} + \widehat {ANF} + \widehat {NCF} = 180^\circ\) (tổng ba góc trong tam giác)
\( \Rightarrow \widehat {NFC} + 45^\circ = 180^\circ \Rightarrow \widehat {NFC} = 135^\circ\)
