
Cho tam giác DEF vuông tại D có \(\widehat F = {30^o}\) . Đường trung trực của EF cắt DF tại M. Chứng minh rằng EM là tia phân giác của góc DEF.

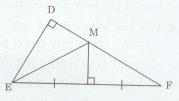
∆DEF vuông tại D có \(\widehat {DEF} + \widehat F = 90^\circ \Rightarrow \widehat {DEF} + 30^\circ = 90^\circ \Rightarrow \widehat {DEF} = 60^\circ\)
M thuộc đường trung trực của EF (gt)
Advertisements (Quảng cáo)
=> ME = MF => ∆MEF cân tại M \( \Rightarrow \widehat {MEF} = \widehat F\)
Mà \(\widehat F = 30^\circ\). Nên \(\widehat {MEF} = 30^\circ .\)
Ta có \(\widehat {MED} + \widehat {MEF} = \widehat {DEF}\)
Nên \(\widehat {MED} + 30^\circ = 60^\circ \Rightarrow \widehat {MED} = 60^\circ - 30^\circ = 30^\circ\)
Do đó \(\widehat {MED} = \widehat {MEF}( = 30^\circ )\). Vậy EM là tia phân giác của góc DEF.
