I. Trường hợp bằng nhau góc – cạnh – góc (g.c.g)
HĐ 2
Cho hai tam giác ABC và A’B’C’ (Hình 57) có:\(\widehat A = \widehat {A’} = 60^\circ \), AB = A’B’ = 3 cm, \(\widehat B = \widehat {B’} = 45^\circ \). Bằng cách đếm số ô vuông, hãy so sánh BC và B’C’. Từ đó có thể kết luận được hai tam giác ABC và A’B’C’ bằng nhau hay không?
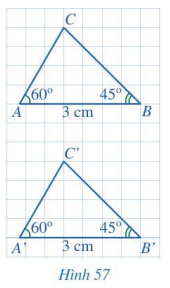

Đếm số ô vuông của cạnh BC và B’C’ rồi xem hai tam giác ABC và A’B’C’ có bằng nhau không.

BC = B’C’ = 4 (đường chéo của 4 ô vuông).
Tam giác ABC và tam giác A’B’C’ có: BC = B’C’, AB = A’B’, \(\widehat B = \widehat {B’}\).
Vậy \(\Delta ABC = \Delta A’B’C’\)(c.g.c)
LT - VD 1
Cho hai tam giác ABC và A’B’C’ thỏa mãn: BC = B’C’ = 3 cm, \(\widehat B = \widehat {B’} = 60^\circ ,\widehat C = 50^\circ ,\widehat {A’} = 70^\circ \). Hai tam giác ABC và A’B’C’ có bằng nhau không? Vì sao?

Ta so sánh hai tam giác ABC và A’B’C’.

Advertisements (Quảng cáo)
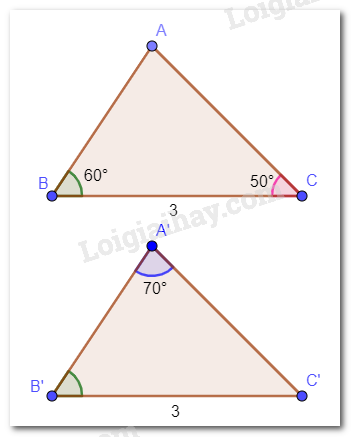
Tổng ba góc trong một tam giác bằng 180°. Vậy trong tam giác A’B’C’ có \(\widehat {C’} = 180^\circ - 70^\circ - 60^\circ = 50^\circ \).
Xét hai tam giác ABC và A’B’C’ có:
\(\widehat B = \widehat {B’} = 60^\circ ;\)
BC = B’C’ ( = 3 cm)
\(\widehat C = \widehat {C’} = 50^\circ \)
Vậy \(\Delta ABC = \Delta A’B’C’\)(g.c.g)
LT - VD 2
Giải thích bài toán ở phần mở đầu.

Chứng minh tam giác ABC bằng tam giác ABD theo trường hợp góc cạnh góc.
Nếu một cạnh và hai góc liền kề cạnh đó của tam giác này bằng một cạnh và hai góc liền kề tương ứng của tam giác kia thì hai tam giác này bằng nhau.

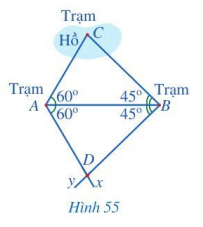
Xét hai tam giác ABC và ABD có: \(\widehat {CAB} = \widehat {DAB} = 60^\circ ,\widehat {ABC} = \widehat {ABD} = 45^\circ \), AB chung.
Vậy \(\Delta ABC = \Delta ABD\) (g.c.g).
Suy ra AC = AD và BC = BD ( 2 cạnh tương ứng)
