Bài 39 Cho hình thang ABCD(AB//CD). Gọi O là giao điểm của hai đường chéo AC và BD.. Bài 39 trang 79 – Sách giáo khoa toán 8 tập 2 – Trường hợp đồng dạng thứ ba
Advertisements (Quảng cáo)
Bài 39 Cho hình thang ABCD(AB//CD). Gọi O là giao điểm của hai đường chéo AC và BD.
a) Chứng minh rằng OA.OD = OB.OC.
b) Đường thẳng qua O vuông góc với AB và CD theo thứ tự tại H và K.
Chứng minh rằng \(\frac{OH}{OK}\) = \(\frac{AB}{CD}\)
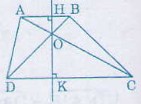
a) Vì AB // CD => ∆AOB ∽ ∆COD
=> \(\frac{OA}{OC}\) = \(\frac{OB}{OD}\) => OA.OD = OC.OB
b) ∆AOH và ∆COK có:
\(\widehat{AHO}\) = \(\widehat{CKO}\) = 900
\(\widehat{HOA}\) = \(\widehat{KOC}\)
=> ∆AOH ∽ ∆COK
=> \(\frac{OH}{OK}\) = \(\frac{OA}{OC}\) (1)
mà \(\frac{OA}{OC}\) = \(\frac{AB}{CD}\) (2)
Từ 1 và 2 => \(\frac{OH}{OK}\) = \(\frac{AB}{CD}\)