Bài 44. Cho tam giác ABC có các cạnh AB= 24cm, AC = 28cm. Tia phân giác của góc A cắt cạnh BC tại D. Gọi M,N theo thứ tự là hình chiếu của B và C trên AD.
a) Tính tỉ số \(\frac{BM}{CN}\)
b) Chứng minh rằng \(\frac{AM}{AN}\) = \(\frac{DM}{DN}\)

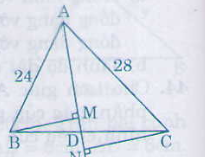
a) AD là đường phân giác của ∆ABC
=> \(\frac{DB}{DC}\) = \(\frac{AB}{AC}\) = \(\frac{DB}{DC}\) = \(\frac{24}{28}\) = \(\frac{6}{7}\)
Mà BM // CN (cùng vuông góc với AD).
=> ∆BMD ∽ ∆CND => \(\frac{BM}{CN}\) = \(\frac{BD}{CD}\)
Advertisements (Quảng cáo)
Vậy \(\frac{BM}{CN}\) = \(\frac{6}{7}\)
b) ∆ABM và ∆ACN có: \(\widehat{ABM}\) = \(\widehat{CAN}\)
\(\widehat{BMA}\) = \(\widehat{CNA}\) = 900
=> ∆ABM ∽ ∆ACN => \(\frac{AM}{AN}\) = \(\frac{AB}{AC}\).
mà \(\frac{AB}{AC}\) = \(\frac{DB}{DC}\) (cmt)
và \(\frac{BD}{CD}\) = \(\frac{DM}{DN}\)
=> \(\frac{AM}{AN}\) = \(\frac{DM}{DN}\)
