
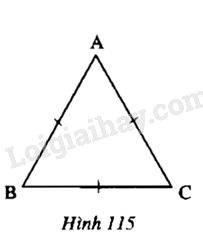
Vẽ tam giác đều \(ABC\) (hình 115)
a) Vì sao \(\widehat B = \widehat C;\,\,\widehat C = \widehat A\) ?
b) Tính số đo mỗi góc của tam giác \(ABC\).
Tam giác đều là tam giác có ba cạnh bằng nhau.
Tam giác cân có hai góc đáy bằng nhau.
Định lí: Tổng ba góc của một tam giác bằng \(180^o\).

Advertisements (Quảng cáo)
Tam giác \(ABC\) đều \( \Rightarrow AB = BC = CA\)
a) Xét tam giác \(ABC\) cân tại \(A\) \( \Rightarrow \widehat B = \widehat C\)
Xét tam giác \(ABC\) cân tại \(B\) \(\Rightarrow \widehat C = \widehat A\)
\(\Rightarrow \widehat A = \widehat B = \widehat C\)
b) Áp dụng định lí tổng các góc của một tam giác vào tam giác \(ABC\) ta có:
\(\widehat A + \widehat B + \widehat C = {180^o}\)
Mà \( \widehat A = \widehat B = \widehat C\) (chứng minh trên)
\( \Rightarrow \widehat A = \widehat B = \widehat C = \dfrac{{{{180}^o}}}{3} = {60^o}\)
Tam giác \(ABC\) có ba góc bằng nhau và bằng \(60^o\).
