
Bài 2 (4.24). Cho tam giác ABC cân tại A và M là trung điểm của BC. Chứng minh AM vuông góc với BC và AM là tia phân giác của góc BAC.
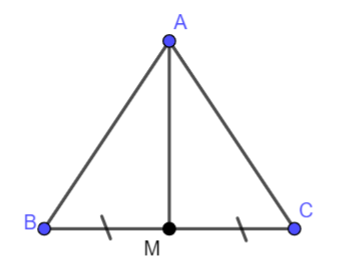

Chứng minh \(\widehat {AMB} = {90^o}\) và AM là tia phân giác của góc BAC .

|
GT |
\(\Delta ABC\)cân tại A, \(M \in BC,MB = MC.\) |
|
Advertisements (Quảng cáo) KL |
\(AM \bot BC,\widehat {MAB} = \widehat {MAC}\) |
Xét tam giác ABM và ACM ta có:
AB = AC (do \(\Delta ABC\)cân tại A)
\(\widehat {ABM} = \widehat {ACM}\) (do \(\Delta ABC\)cân tại A)
MB = MC (theo giả thiết)
Vậy \(\Delta ABM = \Delta ACM\)(c – g – c). Do đó \(\widehat {MAB} = \widehat {MAC}\) hay AM là tia phân giác của góc BAC.
Đồng thời \(\widehat {AMB} = \widehat {AMC} = \frac{{\widehat {AMB} + \widehat {AMC}}}{2} = \frac{{{{180}^o}}}{2} = {90^o}\) hay \(AM \bot BC.\)
