
Bài 3 (4.25). Cho tam giác ABC và M là trung điểm BC.
a) Giả sử AM vuông góc với BC. Chứng minh rẳng \(\Delta ABC\)cân tại A.
b) Giả sử AM là tia phân giác của góc BAC. Chứng minh rẳng \(\Delta ABC\)cân tại A.

Tam giác cân là tam giác có hai cạnh bằng nhau.

a)
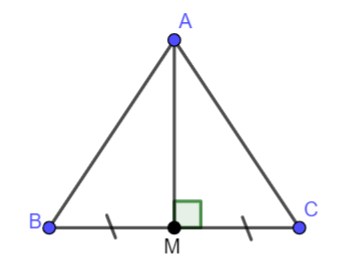
|
GT |
\(\Delta ABC\), \(M \in BC,MB = MC,AM \bot BC\) |
|
KL |
\(\Delta ABC\)cân tại A |
Ta thấy hai tam giác ABM và ACM vuông tại đỉnh M và có:
MB = MC
AM là cạnh chung
Advertisements (Quảng cáo)
Vậy \(\Delta ABM = \Delta ACM\)(hai cạnh góc vuông). Do đó AB = AC hay \(\Delta ABC\)cân tại A.
b)
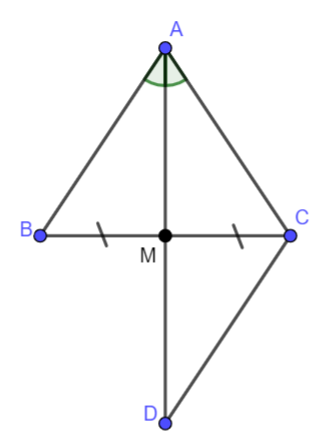
|
GT |
\(\Delta ABC\), \(M \in BC,MB = MC,\widehat {MAB} = \widehat {MAC}\) |
|
KL |
\(\Delta ABC\)cân tại A |
Kéo dài AM một đoạn MD sao cho MD = MA.
Hai tam giác MAB và MDC có
MB = MC (theo giả thiết)
\(\widehat {AMB} = \widehat {CMD}\)(hai góc đối đỉnh)
MA = MD (theo cách dựng)
Vậy \(\Delta MAB = \Delta MDC\)(c – g – c). Do đó AB = DC (1)
Mặt khác \(\Delta ACD\)có \(\widehat {CAD} = \widehat {BAM} = \widehat {CDM} = \widehat {CDA}\)
Vậy \(\Delta ACD\)cân tại C và do đó AC = CD (2)
Từ (1) và (2) suy ra AB = AC hay \(\Delta ABC\)cân tại A.
