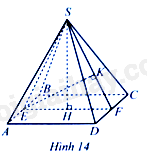
Cho hình chóp tứ giác đều \(S.ABCD\) có chiều cao \(SH\). Gọi \(E,F\) lần lượt là trung điểm của \(AB,CD\). Kẻ \(EK\) vuông góc với \(SF\) tại \(K\) (Hình 14). Biết \(AB = EF = 13cm,SH = EK\). Tính tổng diện tích các mặt của hình chóp tứ giác đều đó.
Áp dụng công thức \({S_{xq}} = \frac{1}{2}.C.d\), trong đó \({S_{xq}}\) là diện tích xung quanh, \(C\) là chu vi đáy, \(d\) là độ dài trung đoạn của hình chóp tứ giác đều. Và công thức tính diện tích tam giác để tính tổng diện tích các mặt của hình chóp tứ giác đều đó.
Ta có diện tích của tam giác \(SEF\) bằng:
\(\frac{1}{2}.SH.EF = \frac{1}{2}.EK.SF\)
Mà \(SH = EK\), suy ra \(SF = EF = 13cm\)
Diện tích xung quanh của hình chóp tứ giác đều \(S.ABCD\) là: \(\frac{1}{2}.\left( {13.4} \right).13 = 338\left( {c{m^2}} \right)\)
Diện tích đáy của hình chóp tứ giác đều \(S.ABCD\) là: \({13^2} = 169\left( {c{m^2}} \right)\)
Tổng diện tích các mặt của hình chóp tứ giác đều \(S.ABCD\) là: \(338 + 169 = 507\left( {c{m^2}} \right)\).