Áp dụng công thức \({S_{xq}} = \frac{1}{2}.C.d\), trong đó \({S_{xq}}\) là diện tích xung quanh, \(C\) là chu vi đáy. Phân tích và lời giải bài 22 trang 79 sách bài tập (SBT) toán 8 - Cánh diều - Bài tập cuối chương IV. Tính diện tích xung quanh của hình chóp tứ giác đều ở mỗi hình 15a, 15b: :...
Tính diện tích xung quanh của hình chóp tứ giác đều ở mỗi hình 15a, 15b:
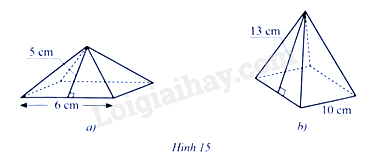
Áp dụng công thức \({S_{xq}} = \frac{1}{2}.C.d\), trong đó \({S_{xq}}\) là diện tích xung quanh, \(C\) là chu vi đáy, \(d\) là độ dài trung đoạn của hình chóp tứ giác đều.
Áp dụng công thức tính diện tích xung quanh của hình chóp tứ giác đều \({S_{xq}} = \frac{1}{2}.C.d\), ta có:
Diện tích xung quanh của hình chóp tứ giác đều ở hình 15a là:
\(\frac{1}{2}.\left( {6.4} \right).5 = 60\left( {c{m^2}} \right)\)
Diện tích xung quanh của hình chóp tứ giác đều ở hình 15b là:
\(\frac{1}{2}.\left( {10.4} \right).13 = 260\left( {c{m^2}} \right)\)