Áp dụng trường hợp đồng dạng thứ ba: góc – góc Nếu hai góc của tam giác này lần lượt bằng hai góc của tam giác kia thì hai tam. Lời giải bài tập, câu hỏi bài 45 trang 78 sách bài tập toán 8 – Cánh diều - Bài 8. Trường hợp đồng dạng thứ ba của tam giác. Cho hình thang \(ABCD\) có \(AB//CD\), \(AB = 4\)cm, \(DB = 6\) cm và \(\widehat {DAB} = \widehat {DBC}\)....

Cho hình thang \(ABCD\) có \(AB//CD\), \(AB = 4\)cm, \(DB = 6\) cm và \(\widehat {DAB} = \widehat {DBC}\). Tính độ dài \(CD\).

Áp dụng trường hợp đồng dạng thứ ba: góc – góc
Nếu hai góc của tam giác này lần lượt bằng hai góc của tam giác kia thì hai tam giác đó đồng dạng.
Advertisements (Quảng cáo)

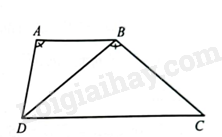
Ta có: \(\widehat {DAB} = \widehat {DBC}\) (giả thiết), \(\widehat {ABD} = \widehat {BDC}\) (hai góc so le trong). Suy ra \(\Delta ABD\backsim \Delta BDC\).
Do đó ta có \(\frac{{AB}}{{BD}} = \frac{{BD}}{{DC}}\), tức là \(CD = \frac{{B{D^2}}}{{AB}}\)
Từ đó: \(CD = \frac{{{6^2}}}{4} = 9\) (cm)
