
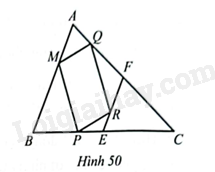
Cho tam giác \(ABC\) có \(E,F\) lần lượt là trung điểm của \(BC,AC\). Các điểm \(M,P,R,Q\) lần lượt nằm trên \(AB,BE,EF,FA\) sao cho \(\frac{{BM}}{{MA}} = \frac{{QF}}{{QA}} = \frac{{RF}}{{RE}} = \frac{{BP}}{{PE}} = 1,8\) (Hình 50).
Tìm khẳng định sai trong các khẳng định sau:
a) Hai đoạn thẳng \(EF\) và \(AB\) đồng dạng phối cảnh, điểm \(C\) là tâm đồng dạng phối cảnh.
b) Hai đoạn thẳng \(MP\) và \(AE\) đồng dạng phối cảnh, điểm \(B\) là tâm đồng dạng phối cảnh và \(\frac{{BM}}{{BA}} = \frac{{BP}}{{BE}} = \frac{3}{5}\).
c) Hai đoạn thẳng \(PR\) và \(BF\) đồng dạng phối cảnh, điểm \(E\) là tâm đồng dạng phối cảnh.
Advertisements (Quảng cáo)

Bằng cách “phóng to” (nếu tỉ số vị tự \(k > 1\)) hay “thu nhỏ” (nếu tỉ số vị tự \(k < 1\)) hình \(H\), ta sẽ nhận được hình \(H'\) đồng dạng phối cảnh (hay vị tự) với hình \(H\).
Ta gọi hình \(H’\) là hình đồng dạng phối cảnh (hay vị tự) tỉ số \(k\) của hình \(H\)
Hình đồng dạng phối cảnh tỉ số k của đoạn thẳng \(AB\) là một đoạn thẳng \(A’B’\) (nằm trên đường thẳng song song hoặc trùng với đường thẳng \(AB\)) và \(A’B’ = k.AB\)

Ta có \(\frac{{BM}}{{MA}} = \frac{9}{5} = > \frac{{BM}}{{BA}} = \frac{9}{{14}}\)
Vậy khẳng định b) sai.
