
Hình 54 cho biết \(A’B’=4,A’O=3,AO=6,OB=x,AB=y\)Giá trị của biểu thức \(x+y\) là: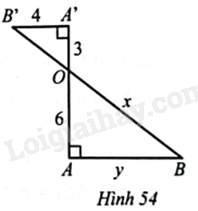 A. 22B. 18C. 20D. 16
A. 22B. 18C. 20D. 16 
Tam giác \(A’B’C’\) gọi là đồng dạng với tam giác \(ABC\) nếu:
\(\widehat{A’}=\widehat{A},\widehat{B’}=\widehat{B},\widehat{C’}=\widehat{C}\) ; \(\frac{A’B’}{AB}=\frac{B’C’}{BC}=\frac{A’C’}{AC}\).
Kí hiệu là \(\Delta A’B’C’\backsim \Delta ABC\).
Tỉ số các cạnh tương ứng \(\frac{A’B’}{AB}=\frac{B’C’}{BC}=\frac{C’A’}{CA}=k\) gọi là tỉ số đồng dạng.

Chọn đáp án B
Advertisements (Quảng cáo)
Tam giác vuông \(A’B’O\) vuông tại \(A’\) nên theo định lí Pythagore, ta có:
\( B'{{O}^{2}}=A’B{{‘}^{2}}+A'{{O}^{2}}=42+32=25 \\ =>B’O=5 \)
Xét hai tam giác vuông \(ABO\) và \(A’B’O\) có: \(\widehat{A}=\widehat{A’}=90{}^\circ ;\widehat{AOB}=\widehat{A’OB’}\) (hai góc đối đỉnh).
\(=>\Delta ABO\backsim \Delta A’B’O\) (g.g)
\(=>\frac{AB}{A’B’}=\frac{BO}{B’O}=\frac{AO}{A’O}\)
Hay \(\frac{y}{4}=\frac{x}{5}=\frac{6}{3}\)
\(=>y=\frac{4.6}{3}=8;x=\frac{5.6}{3}=10\)
Vậy \(x+y=10+8=18\).
