
Gọi O là giao điểm của hai đường chéo hình bình hành ABCD. Với mỗi tam giác OAB, OBC, OCD, ODA, xét giao điểm ba đường phân giác của tam giác đó. Tại sao bốn điểm vừa vẽ là bốn đỉnh của một hình thoi?

Sử dụng kiến thức về dấu hiệu nhận biết hình thoi để chứng minh: Hình bình hành có hai đường chéo vuông góc với nhau là hình thoi.

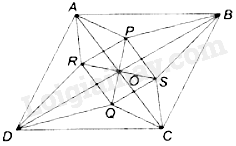
Gọi P, Q lần lượt là giao điểm ba đường phân giác của tam giác OAB, OCD thì O, P, Q cùng nằm trên đường phân giác của góc AOB.
Do ABCD là hình bình hành nên
+ \(OB = OD\)
+ AB//CD, AD//BC
Suy ra: \(\widehat {ODC} = \widehat {OBA};\widehat {OCD} = \widehat {OAB}\) (so le trong)
Advertisements (Quảng cáo)
Mà DQ, BP lần lượt là tia phân giác của góc ODC và góc OBA nên \(\widehat {OBP} = \widehat {ODQ}\)
Tam giác OBP và tam giác ODQ có:
\(\widehat {OBP} = \widehat {ODQ}\), \(OB = OD\), \(\widehat {BOP} = \widehat {QOD}\) (đối đỉnh)
Do đó, \(\Delta OBP = \Delta ODQ\left( {g - c - g} \right)\)
Suy ra \(OP = OQ\) hay O là trung điểm của PQ.
Gọi R, S lần lượt là giao điểm ba đường phân giác của tam giác OAD, OBC.
Chứng minh tương tự, ta có O là trung điểm của RS, đường thẳng RS là đường phân giác của góc AOD.
Ta có: \(\widehat {AOB} + \widehat {AOD} = {180^0}\)
Nên \(\widehat {POA} + \widehat {ROA} = {90^0}\) hay \(PQ \bot RS\) tại O.
Tứ giác PSQR có: O là trung điểm của PQ, O là trung điểm của RS nên PSQR là hình bình hành.
Mà \(PQ \bot RS\) tại O. Do đó, PSQR là hình thoi.
