
Cho hình vuông ABCD. Với điểm M nằm giữa C và D, kẻ tia phân giác của góc DAM; nó cắt CD ở N. Đường thẳng qua N vuông góc với AM cắt BC ở P. Tính số đo của góc NAP.

Sử dụng tính chất của hình vuông để tính số đo góc NAP: Hình vuông có bốn góc vuông và các cạnh bằng nhau.

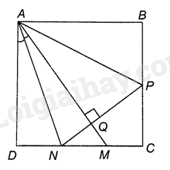
Vì ABCD là hình vuông nên \(\widehat {ADN} = \widehat {ABP} = {90^0}\) và \(AB = AD\)
Gọi Q là giao điểm của NP và AM.
Vì \(NP \bot AM\) tại Q nên \(\widehat {AQN} = \widehat {AQP} = {90^0}\)
Advertisements (Quảng cáo)
Tam giác AND và tam giác ANQ có:
\(\widehat {ADN} = \widehat {AQN} = {90^0}\), AN chung, \(\widehat {DAN} = \widehat {QAN}\) (do AN là tia phân giác của góc DAM)
Do đó, \(\Delta ADN = \Delta AQN\left( {ch - gn} \right)\) nên \(AD = AQ\)
Mà \(AB = AD\) (cmt) nên \(AQ = AB\)
Tam giác AQP và tam giác ABP có:
\(\widehat {AQP} = \widehat {ABP} = {90^0}\), AP chung, \(AQ = AB\) (cmt)
Do đó, \(\Delta AQP = \Delta ABP\left( {ch - cgv} \right)\), suy ra: \(\widehat {QAP} = \widehat {PAB}\)
Ta có: \(\widehat {QAP} + \widehat {PAB} + \widehat {DAN} + \widehat {QAN} = {90^0}\)
Nên \(2\left( {\widehat {QAP} + \widehat {QAN}} \right) = {90^0}\), tức là \(\widehat {NAP} = {45^0}\)
