
Chứng minh tổng độ dài hai đường chéo của tứ giác:
a) Bé hơn chu vi của tứ giác;
b) Lớn hơn tổng hai cạnh đối tùy ý của tứ giác, từ đó lớn hơn nửa chu vi của tứ giác.

Áp dụng định lý bất đẳng thức trong tam giác.

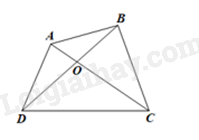
Xét tứ giác ABCD. Chu vi tứ giác ABCD là \({P_{ABCD}}\; = AB + BC + CD + DA\).
a) Trong \(\Delta ABC\) có \(AC < AB + BC\) (bất đẳng thức trong tam giác)
Trong \(\Delta ACD\) có \(AC < CD + DA\) (bất đẳng thức trong tam giác)
Do đó \(AC + AC < AB + BC + \;CD + DA\) hay \(2AC < {P_{ABCD}}\;\) (1)
Tương tự, trong \(\Delta ABD\) có \(BD < AD + AB\)
Advertisements (Quảng cáo)
Trong \(\Delta BCD\) có: \(BD < CD + BC\)
Do đó \(BD + BD < AD + AB + CD + BC\) hay \(2BD < {P_{ABCD}}\). (2)
Từ (1) và (2) suy ra \(2\left( {AC + BD} \right) < 2{P_{ABCD}}\), do đó \(AC + BD < {P_{ABCD}}\).
b) Gọi O là giao điểm của AC và BD.
Trong \(\Delta OAB\) có \(OA + OB > AB\) (bất đẳng thức trong tam giác)
Trong \(\Delta OCD\) có \(OC + OD > CD\) (bất đẳng thức trong tam giác)
Nên \(AC + BD = OA + OC + OB + OD > AB + CD\).
Trong \(\Delta OAD\) có \(OA + OD > AD\) (bất đẳng thức trong tam giác)
Trong \(\Delta OBC\) có \(OB + OC > BC\) (bất đẳng thức trong tam giác)
Nên \(AC + BD = OA + OC + OB + OD > AD + BC\).
Vậy \(2\left( {AC + BD} \right) > AB + BC + CD + DA = {P_{ABCD}}\)
Tức là \(AC + BD\; > \frac{1}{2}{P_{ABCD}}\) (đpcm).
