
Tìm điểm M bên trong tứ giác ABCD sao cho tổng khoảng cách từ M đến bốn đỉnh A, B, C, D là bé nhất.

Sử dụng bất đẳng thức tam giác: Trong một tam giác, tổng hai cạnh luôn lớn hơn cạnh còn lại

Trước hết cho hai điểm phân biệt P, Q thì với mọi điểm M ta có \(MP + MQ \ge PQ\) và \(MP + MQ = PQ\) chỉ khi M thuộc đoạn thẳng PQ.
Thật vậy,
• Nếu M không thuộc đường thẳng PQ thì \(MP + MQ > PQ\) (bất đẳng thức tam giác) (hình vẽ)
• Nếu M thuộc đoạn thẳng PQ thì \(MP + MQ = PQ\) (hình vẽ)
Advertisements (Quảng cáo)

• Nếu M thuộc đường thẳng PQ nhưng không thuộc đoạn thẳng PQ thì hoặc P nằm giữa M và Q hoặc Q nằm giữa P và M, dễ thấy trong cả hai trường hợp đó, \(MP + MQ > PQ\) (hình vẽ).

– Xét điểm M tuỳ ý trong tứ giác ABCD (hình vẽ).
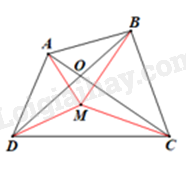
Ta có:
\(MA + MC \ge AC\) và \(MA + MC = AC\) khi điểm M nằm trên đoạn thẳng AC.
\(MB + MD \ge BD\) và \(MB + MD = BD\) khi điểm M nằm trên đoạn thẳng BD.
Do đó \(MA + MB + MC + MD \ge AC + BD\) và \(MA + MB + MC + MD = AC + BD\) chỉ khi M vừa thuộc đoạn thẳng AC vừa thuộc đoạn thẳng BD tức là M phải trùng với giao điểm O của AC và BD.
