
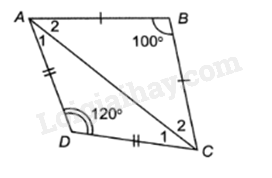
Cho tứ giác ABCD với AB = BC, CD = DA, \(\widehat B = {100^ \circ }\), \(\widehat D = {120^ \circ }\). Tính \(\widehat A\) và \(\widehat C\).

Sử dụng tính chất: Trong một tam giác cân, hai góc ở đáy bằng nhau.
Áp dụng định lý tổng 3 góc trong tam giác bằng \({180^ \circ }\).
Áp dụng định lí tổng các góc trong một tứ giác bằng \({360^ \circ }\).

Advertisements (Quảng cáo)
Do AB = BC nên \(\Delta BAC\) cân tại B, suy ra \(\widehat {{A_2}} = \widehat {{C_2}}\).
Do đó \(\widehat {{A_2}} = \widehat {{C_2}} = \frac{{180^\circ - \widehat B}}{2} = \frac{{180^\circ - 100^\circ }}{2} = 40^\circ \).
Do CD = DA, \(\Delta DAC\) cân tại D, suy ra \(\widehat {{A_1}} = \widehat {{C_1}}\)
Xét \(\Delta DAC\) có: \(\widehat {{A_1}} + \widehat {{C_1}} + \widehat D = 180^\circ \)
Do đó \(\widehat {{A_1}} = \widehat {{C_1}} = \frac{{180^\circ - \widehat D}}{2} = \frac{{180^\circ - 120^\circ }}{2} = 30^\circ \).
Ta có: \(\widehat A = \widehat {{A_1}} + \widehat {{A_2}} = 40^\circ + 30^\circ = 70^\circ \)
\(\widehat C = \widehat {{C_1}} + \widehat {{C_2}} = 40^\circ + 30^\circ = 70^\circ \).
Vậy tứ giác ABCD có \(\widehat A = \widehat C = 70^\circ \).
