b. Hình bình hành ABCD có hai đường cao AH , AK bằng nhau. Chứng minh rằng ABCD là hình thoi.
. Câu 136 trang 97 Sách bài tập (SBT) Toán 8 tập 1 - Bài 11. Hình thoi
a. Cho hình thoi ABCD. Kẻ hai đường cao AH, AK. Chứng minh rằng AH = AK
b. Hình bình hành ABCD có hai đường cao AH , AK bằng nhau. Chứng minh rằng ABCD là hình thoi.

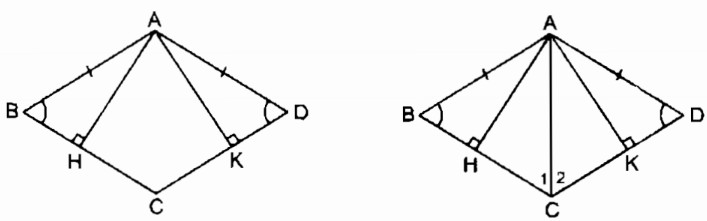
a. Xét hai tam giác vuông AHB và AKD:
\(\widehat {AHB} = \widehat {AKD} = {90^0}\)
AB = AD (gt)
\(\widehat B = \widehat D\) (tính chất hình thoi)
Do đó: ∆ AHB = ∆ AKD (cạnh huyền, góc nhọn)
Advertisements (Quảng cáo)
⇒ AH = AK
b. Xét hai tam giác vuông AHC và AKC:
\(\widehat {AHC} = \widehat {AKC} = {90^0}\)
AH = AK (gt)
AC cạnh huyền chung
Do đó: ∆ AHC = ∆ AKC (cạnh huyền, góc nhọn)
\( \Rightarrow \widehat {ACH} = \widehat {ACK}\) hay \(\widehat {ACB} = \widehat {ACD}\)
⇒ CA là tia phân giác \(\widehat {BCD}\)
Hình bình hành ABCD có đường chéo CA là tia phân giác nên là hình thoi.
