
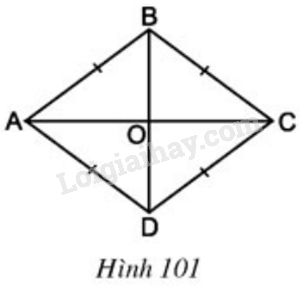
Cho hình thoi \(ABCD\), hai đường chéo cắt nhau tại \(O\) (h.\(101\)).
a) Theo tính chất của hình bình hành, hai đường chéo của hình thoi có tính chất gì ?
b) Hãy phát hiện thêm các tính chất khác của hai đường chéo \(AC\) và \(BD.\)
Áp dụng: Xét hai tam giác bằng nhau.

a) Theo tính chất của hình bình hành, hai đường chéo của hình thoi có tính chất cắt nhau tại trung điểm mỗi đường.
b) Xét \(ΔAOB\) và \(ΔCOB\)
+) \(AB = CB\)
Advertisements (Quảng cáo)
+) \(BO\) chung
+) \(OA = OC\) (\(O\) là trung điểm \(AC\) )
\(⇒ ΔAOB = ΔCOB\;\; (c.c.c)\)
\(⇒ \widehat {ABO} = \widehat {CBO};\,\,\widehat {AOB} = \widehat {COB}\) (các cặp góc tương ứng)
\(\widehat {ABO} = \widehat {CBO} ⇒ BO\) là phân giác góc \(ABC\).
\(\eqalign{
& \widehat {AOB} + \widehat {COB} = {180^o} \cr
& \Rightarrow \widehat {AOB} = \widehat {COB} = {180^o}:2 = {90^o} \cr} \)
\( \Rightarrow AC \bot BD\)
Chứng minh tương tự, ta kết luận được:
\(AC, BD\) là các đường phân giác của các góc của hình thoi và \(AC ⊥ BD\) tại \(O\).
