Hình thoi ABCD có \(\widehat A = {60^0}\) . Trên cạnh AD lấy điểm M, trên cạnh DC lấy điểm N sao cho AM = DN. Tam giác BMN là tam giác gì ? Vì sao ?
Giải:
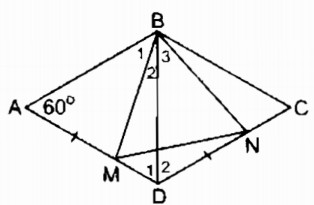
Nối BD, ta có:
AB = AD (gt)
nên ∆ ABD cân tại A
mà \(\widehat A = {60^0}\)
⇒ ∆ ABD đều
\( \Rightarrow \widehat {ABD} = {\widehat D_1} = {60^0}\) và BD = AB
Suy ra: BD = BC = CD
⇒ ∆ CBD đều
Advertisements (Quảng cáo)
\( \Rightarrow {\widehat D_2} = {60^0}\)
Xét ∆ BAM và ∆ BDN:
AB = BD (chứng minh trên)
\(\widehat A = {\widehat D_2} = {60^0}\)
AM = DN
Do đó: ∆ BAM = ∆ BDN (c.g.c) \( \Rightarrow {\widehat B_1} = {\widehat B_3}\) và BM = BN
Suy ra: ∆ BMN cân tại B
\({\widehat B_2} + {\widehat B_1} = \widehat {ABD} = {60^0}\)
Suy ra: \({\widehat B_2} + {\widehat B_3} = \widehat {MBN} = {60^0}\)
Vậy ∆ BMN đều
