Cho hình bình hành ABCD, các đường chéo cắt nhau ở O. Gọi E, F, G, H theo thứ tự là giao điểm của các đường phân giác của các tam giác AOB, BOC, COD, DOA. Chứng minh rằng EFGH là hình thoi.
Giải:
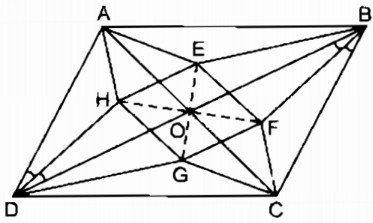
Ta có: \(\widehat {AOB} = \widehat {COD}\) (đối đỉnh)
\(\widehat {EOB} = {1 \over 2}\widehat {AOB}\) (gt)
\(\widehat {COG} = {1 \over 2}\widehat {COD}\) (gt)
Suy ra: \(\widehat {EOB} = \widehat {COG}\)
\(\widehat {EOB} + \widehat {BOC} + \widehat {COG} = 2\widehat {EOB} + \widehat {BOC}\)
mà \(\widehat {AOB} + \widehat {BOC} = {180^0}\) (kề bù)
hay \(2\widehat {EOB} + \widehat {BOC} = {180^0}\)
Suy ra: E, O, G thẳng hàng
Ta lại có: \(\widehat {BOC} = \widehat {AOD}\) (đối đỉnh)
\(\widehat {HOD} = {1 \over 2}\widehat {AOD}\) (gt)
\(\widehat {FOC} = {1 \over 2}\widehat {BOC}\) (gt)
Suy ra: \(\widehat {HOD} = \widehat {FOC}\)
\(\widehat {HOD} + \widehat {COD} + \widehat {FOC} = 2\widehat {HOD} + \widehat {COD}\)
mà \(\widehat {AOD} + \widehat {COD} = {180^0}\) (kề bù)
hay\(2\widehat {HOD} + \widehat {COD} = {180^0}\)
Suy ra: H, O, F thẳng hàng
\(\widehat {ADO} = \widehat {CBO}\) (so le trong)
\(\widehat {HDO} = {1 \over 2}\widehat {ADO}\) (gt)
\(\widehat {FBO} = {1 \over 2}\widehat {CBO}\) (gt)
Advertisements (Quảng cáo)
Suy ra: \(\widehat {HDO} = \widehat {FBO}\)
- Xét ∆ BFO và ∆ DHO:
\(\widehat {HDO} = \widehat {FBO}\) (chứng minh trên_
OD = OB (tính chất hình bình hành)
\(\widehat {HOD} = \widehat {FOB}\) (đối đỉnh)
Do đó: ∆ BFO = ∆ DHO (g.c.g)
⇒ OF = OH
\(\widehat {OAB} = \widehat {OCD}\) (so le trong)
\(\widehat {OAE} = {1 \over 2}\widehat {OAB}\) (gt)
\(\widehat {OCG} = {1 \over 2}\widehat {OCD}\) (gt)
Suy ra: \(\widehat {OAE} = \widehat {OCG}\)
- Xét ∆ OAE và ∆ OCG:
\(\widehat {OAE} = \widehat {OCG}\) (chứng minh trên)
OA = OC (tính chất hình bình hành)
\(\widehat {EOA} = \widehat {GOC}\) (đối đỉnh)
Do đó: ∆ OAE = ∆ OCG (g.c.g)
⇒ OE = OG
Suy ra: Tứ giác EFGH là hình bình hành (vì có hai đường chéo cắt nhau tại trung điểm mỗi đường)
OE ⊥ OF (tính chất hai góc kề bù)
hay EG ⊥ FH
Vậy: Tứ giác EFGH là hình thoi.
