Advertisements (Quảng cáo)
Tam giác ABC có AB = 12cm, AC = 20cm, BC = 28cm. Đường phân giác góc A cắt BC tại D. Qua D kẻ DE // AB (E thuộc AC)
a. Tính độ dài đoạn thẳng BD, DC và DE
b. Cho biết diện tích tam giác ABC là S, tính diện tích các tam giác ABD, ADE và DCE.
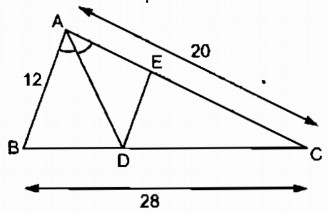
a. Trong tam giác ABC, ta có:
AD là đường phân giác của \(\widehat {BAC}\)
Suy ra: \({{DB} \over {DC}} = {{AB} \over {AC}}\) (tính chất tia phân giác)
Suy ra: \({{DB} \over {DB + DC}} = {{AB} \over {AB + AC}}\)
Suy ra: \({{DB} \over {BC}} = {{AB} \over {AB + AC}}\)
Suy ra: \(DB = {{BC.AB} \over {AB + AC}} = {{28.12} \over {12 + 20}} = {{21} \over 2} = 10,5\) (cm)
Vậy DC = BC – DB = 28 – 10,5 = 17,5 (cm)
Trong tam giác ABC, ta có: DE // AB
Advertisements (Quảng cáo)
Suy ra: \({{DC} \over {DB}} = {{DE} \over {AB}}\) (Hệ quả định lí Ta-lét )
Vậy: \(DE = {{DC.AB} \over {BC}} = {{17,5.12} \over {28}} = 7,5\) (cm0
b. Vì ∆ABD và ∆ABC có chung đường cao kẻ từ đỉnh A nên:
\({{{S_{ABD}}} \over {{S_{ABC}}}} = {{DB} \over {BC}} = {{{{21} \over 2}} \over {28}} = {{21} \over {56}} = {3 \over 8}\)
Vậy : \({S_{ABD}} = {3 \over 8}S\)
\({S_{ADC}} = {S_{ABC}} – {S_{ABD}} = S – {3 \over 8}S = {8 \over 8}S – {3 \over 8}S = {5 \over 8}S\)
Vì DE // AB và AD là đường phân giác góc A nên AE = DE.
Ta có: \({{{S_{ADE}}} \over {{S_{ADC}}}} = {{AE} \over {AC}} = {{DE} \over {AC}} = {{7,5} \over {20}}\)
Vậy: \({S_{ADE}} = {{7,5} \over {20}}.{S_{ADC}} = {{7,5} \over {20}}.{5 \over 8}S = {{7,5} \over {32}}S\)
Ta có: \({S_{DCE}} = {S_{ADC}} – {S_{ADE}} = {5 \over 8}S – {{7,5} \over {32}}S = {{12,5} \over {32}}S\).