Cho tam giác ABC cân tại A. Trên các cạnh bên AB, AC lấy các điểm M, N sao cho BM = CN.
a. Tứ giác BMNC là hình gì ? Vì sao ?
b. Tính các góc của tứ giác BMNC biết rằng \(\widehat A = {40^0}\)

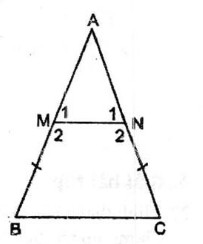
a. ∆ ABC cân tại A
\( \Rightarrow \widehat B = \widehat C = {{{{180}^0} - \widehat A} \over 2}\) (tính chất tam giác cân) (1)
AB = AC (gt)
⇒ AM + BM= AN+ CN
⇒ mà BM = CN (gt)
Advertisements (Quảng cáo)
⇒ suy ra: AM = AN
⇒ ∆ AMN cân tại A
\( \Rightarrow {\widehat M_1} = {\widehat N_1} = {{{{180}^0} - \widehat A} \over 2}\) ( tính chất tam giác cân) (2)
⇒ Từ (1) và (2) suy ra: \({\widehat M_1} = \widehat B\)
⇒MN // BC ( vì có các cặp góc đồng vị bằng nhau)
Tứ giác BCMN là hình thang có \(\widehat B = \widehat C\). Vậy BCMN là hình thang cân.
b. \(\widehat B = \widehat C = {{{{180}^0} - \widehat A} \over 2} = {{{{180}^0} - {{40}^0}} \over 2} = {70^0}\)
Mà \({\widehat M_2} + \widehat B = {180^0}\) (hai góc trong cùng phía)
\( \Rightarrow {\widehat M_2} = {180^0} - \widehat B = {180^0} - {70^0} = {110^0}\)
\({\widehat N_2} = {\widehat M_2} = {110^0}\) (tính chất hình thang cân)
